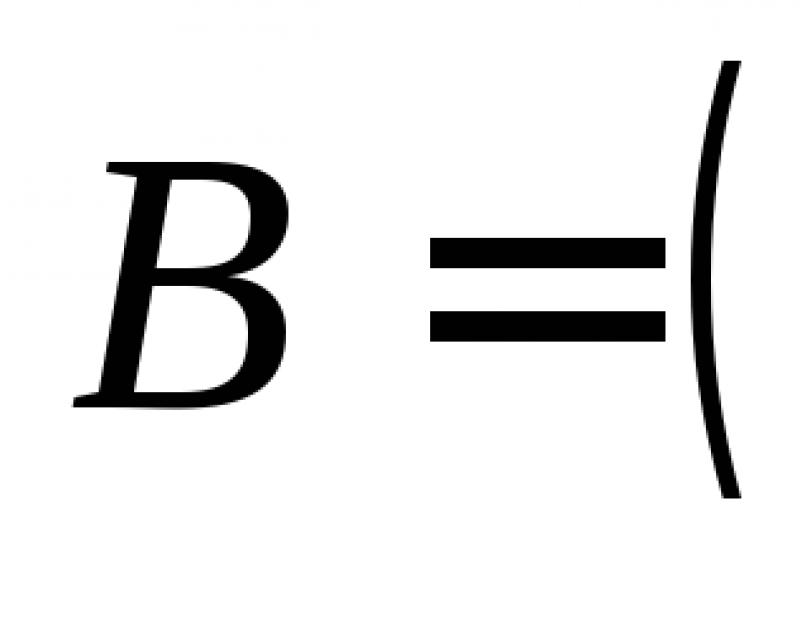Заметим, что строки и столбцы матрицы можно рассматривать как арифметические векторы размеров m и n , соответственно. Таким образом, матрицу размеров можно интерпретировать как совокупностьm n -мерных илиn m -мерных арифметических векторов. По аналогии с геометрическими векторами введем понятия линейной зависимости и линейной независимости строк и столбцов матрицы.

4.8.1. Определение. Строка
называетсялинейной комбинацией строк с коэффициентами
, если для всех элементов этой строки справедливо равенство:

,
.

4.8.2. Определение.

Строки
называютсялинейно зависимыми , если существует их нетривиальная линейная комбинация, равная нулевой строке, т.е. существуют такие не все равные нулю числа

,
.

4.8.3. Определение.

Строки
называютсялинейно независимыми , если только их тривиальная линейная комбинация равна нулевой строке, т.е.

,

4.8.4. Теорема. (Критерий линейной зависимости строк матрицы)

Для того, чтобы строки были линейно зависимыми, необходимо и достаточно, чтобы хотя бы одна из них была линейной комбинацией остальных.

Доказательство:

Необходимость. Пусть строки
линейно зависимы, тогда существует их нетривиальная линейная комбинация, равная нулевой строке:

.

Без ограничения общности предположим, что первый из коэффициентов линейной комбинации отличен от нуля (в противном случае можно перенумеровать строки). Разделив это соотношение на , получим

,

то есть первая строка является линейной комбинацией остальных.

Достаточность. Пусть одна из строк, например, , является линейной комбинацией остальных, тогда

то есть существует нетривиальная линейная комбинация строк
, равная нулевой строке:

а значит, строки
линейно зависимы, что и требовалось доказать.

Замечание.

Аналогичные определения и утверждения могут быть сформулированы и для столбцов матрицы.

§4.9. Ранг матрицы.

4.9.1. Определение. Минором порядка матрицы размера
называется определитель порядка с элементами, расположенными на пересечении некоторых ее строк и столбцов.

4.9.2. Определение. Отличный от нуля минор порядка матрицы размера
называетсябазисным минором , если все миноры матрицы порядка
равны нулю.

Замечание. Матрица может иметь несколько базисных миноров. Очевидно, что все они будут одного порядка. Также возможен случай, когда у матрицы размера
минор порядка отличен от нуля, а миноров порядка
не существует, то есть
.

4.9.3. Определение. Строки (столбцы), образующие базисный минор, называются базисными строками (столбцами).

4.9.4. Определение. Рангом матрицы называется порядок ее базисного минора. Ранг матрицы обозначается
или
.

Замечание.

Отметим, что в силу равноправности строк и столбцов определителя ранг матрицы не меняется при ее транспонировании.

4.9.5. Теорема. (Инвариантность ранга матрицы относительно элементарных преобразований)

Ранг матрицы не меняется при ее элементарных преобразованиях.

Без доказательства.

4.9.6. Теорема. (О базисном миноре).

Базисные строки (столбцы) линейно независимы. Всякая строка (столбец) матрицы может быть представлена в виде линейной комбинации ее базисных строк (столбцов).

Доказательство:

Проведем доказательство для строк. Доказательство утверждения для столбцов может быть проведено по аналогии.

Пусть ранг матрицы размеров
равен, а
− базисный минор. Без ограничения на общность предположим, что базисный минор расположен в левом верхнем углу (в противном случае можно привести матрицу к этому виду с помощью элементарных преобразований):

.

Докажем сначала линейную независимость базисных строк. Доказательство проведем от противного. Предположим, что базисные строки линейно зависимы. Тогда согласно теореме 4.8.4 одна из строк может быть представлена в виде линейной комбинации остальных базисных строк. Следовательно, если вычесть из этой строки указанную линейную комбинацию, то мы получим нулевую строку, а это означает, что минор
равен нулю, что противоречит определению базисного минора. Таким образом, мы получили противоречие, следовательно, линейная независимость базисных строк доказана.

Докажем теперь, что всякая строка матрицы может быть представлена в виде линейной комбинации базисных строк. Если номер рассматриваемой строки от 1 доr , то тогда, очевидно, она может быть представлена в виде линейной комбинации c коэффициентом, равным 1 при строке и нулевыми коэффициентами при остальных строках. Покажем теперь, что если номер строкиот
до
, она может быть представлена в виде линейной комбинации базисных строк. Рассмотрим минор матрицы
, полученный из базисного минора
добавлением строкии произвольного столбца
:

Покажем, что данный минор
от
до
и для любого номера столбцаот 1 до.

Действительно, если номер столбца от 1 доr , то имеем определитель с двумя одинаковыми столбцами, который, очевидно, равен нулю. Если же номер столбца отr +1 до , а номер строкиот
до
, то
является минором исходной матрицы большего порядка, чем базисный минор, а это означает, что он равен нулю из определения базисного минора. Таким образом, доказано, что минор
равен нулю для любого номера строкиот
до
и для любого номера столбцаот 1 до. Разлагая его по последнему столбцу, получим:

Здесь
− соответствующие алгебраические дополнения. Заметим, что
, так как следовательно,
является базисным минором. Следовательно, элементы строкиk могут быть представлены в виде линейной комбинации соответствующих элементов базисных строк с коэффициентами, не зависящими от номера столбца :

Таким образом, мы доказали, что произвольная строка матрицы может быть представлена в виде линейной комбинации ее базисных строк. Теорема доказана.

Лекция 13

4.9.7. Теорема. (О ранге невырожденной квадратной матрицы)

Для того, чтобы квадратная матрица являлась невырожденной, необходимо и достаточно, чтобы ранг матрицы равен размеру этой матрицы.

Доказательство:

Необходимость. Пусть квадратная матрица размераn является невырожденной, тогда
, следовательно, определитель матрицы является базисным минором, т.е.

Достаточность. Пусть
тогда порядок базисного минора равен размеру матрицы, следовательно, базисным минором является определитель матрицы, т.е.
по определению базисного минора.

Следствие.

Для того, чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы ее строки были линейно независимыми.

Доказательство:

Необходимость. Так как квадратная матрица является невырожденной, то ее ранг равен размеру матрицы
то есть определитель матрицы является базисным минором. Следовательно, по теореме 4.9.6 о базисном миноре строки матрицы являются линейно независимыми.

Достаточность. Так как все строки матрицы линейно независимы, то ее ранг не меньше размера матрицы, а значит,
следовательно, по предыдущей теореме 4.9.7 матрицаявляется невырожденной.

4.9.8. Метод окаймляющих миноров для нахождения ранга матрицы.

Заметим, что частично этот метод уже был неявно описан в доказательстве теоремы о базисном миноре.

4.9.8.1. Определение. Минор
называетсяокаймляющим по отношению к минору
, если он получен из минора
добавлением одной новой строки и одного нового столбца исходной матрицы.

4.9.8.2. Процедура нахождения ранга матрицы методом окаймляющих миноров.

Находим какой-либо текущий минор матрицы отличный от нуля.

Вычисляем все окаймляющие его миноры.

Если все они равны нулю, то текущий минор является базисным, и ранг матрицы равен порядку текущего минора.

Если среди окаймляющих миноров находится хотя бы один отличный от нуля, то он полагается текущим и процедура продолжается.

Найдем с помощью метода окаймляющих миноров ранг матрицы

.

Легко указать текущий минор второго порядка, отличный от нуля, например,

.

Вычисляем окаймляющие его миноры:

Следовательно, так как все окаймляющие миноры третьего порядка равны нулю, то минор
является базисным, то есть

Замечание. Из рассмотренного примера видно, что метод является достаточно трудоемким. Поэтому на практике гораздо чаще используется метод элементарных преобразований, речь о котором пойдет ниже.

4.9.9. Нахождение ранга матрицы методом элементарных преобразований.

На основании теоремы 4.9.5 можно утверждать, что ранг матрицы не меняется при элементарных преобразованиях (то есть ранги эквивалентных матриц равны). Поэтому ранг матрицы равен рангу ступенчатой матрицы, полученной из исходной элементарными преобразованиями. Ранг же ступенчатой матрицы, очевидно, равен количеству ее ненулевых строк.

Определим ранг матрицы

методом элементарных преобразований.

Приведем матрицу к ступенчатому виду:

Количество ненулевых строк полученной ступенчатой матрицы равно трем, следовательно,

4.9.10. Ранг системы векторов линейного пространства.

Рассмотрим систему векторов
некоторого линейного пространства. Если она является линейно зависимой, то в ней можно выделить линейно независимую подсистему.

4.9.10.1. Определение. Рангом системы векторов
линейного пространстваназывается максимальное количество линейно независимых векторов этой системы. Ранг системы векторов
обозначается как
.

Замечание. Если система векторов линейно независима, то ее ранг равен количеству векторов системы.

Сформулируем теорему, показывающую связь понятий ранга системы векторов линейного пространства и ранга матрицы.

4.9.10.2. Теорема. (О ранге системы векторов линейного пространства)

Ранг системы векторов линейного пространства равен рангу матрицы, столбцами или строками которой являются координаты векторов в некотором базисе линейного пространства.

Без доказательства.

Следствие.

Для того, чтобы система векторов линейного пространства являлась линейно независимой, необходимо и достаточно, чтобы ранг матрицы, столбцами или строками которой являются координаты векторов в некотором базисе, был равен количеству векторов системы.

Доказательство очевидно.

4.9.10.3. Теорема (О размерности линейной оболочки).

Размерность линейной оболочки векторов
линейного пространстваравна рангу этой системы векторов:

Без доказательства.

Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов. В дальнейшем будем излагать материал для строк, для столбцов изложение аналогично.

В матрице A обозначим ее строки следующим образом:

, , …. ,

Две строки матрицы называются равными , если равны их со­ответствующие элементы: , если , .

Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, прово­димые поэлементно:

Строка е называется линейной комбинацией строк ..., матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:

Строки матрицы называются линейно зависимы­ми , если существуют такие числа , не равные одно­временно нулю, что линейная комбинация строк матрицы равна нулевой строке:

, =(0,0,...,0). (3.3)

Теорема 3.3 Строки матрицы линейно зависимы, если хотя бы одна строка матрицы является линейной комбинацией остальных.

□ Действительно, пусть для определенности в формуле (3.3) , тогда

Таким образом, строка является линейной комбинат остальных строк. ■

Если линейная комбинация строк (3.3) равна нулю тогда и только тогда, когда все коэффициенты равны нулю, то строки называются линейно независимыми.

Теорема 3.4. (о ранге матрицы) Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).

□ Пусть матрица A размера m n имеет ранг r (r min ). Это означает, что существует отличный от нуля минор r -го порядка. Всякий ненулевой минор r -го порядка будем называть базисным минором.

Пусть для определенности базисный минор есть ведущий или угловой минор. Тогда строки матрицы линейно независимы. Предположим противное, то есть одна из этих строк, например , является линейной комбинацией остальных . Вычтем из элементов r - ой строки элементы 1-й строки, умноженные на , затем элементы 2-й строки, умноженные на , … и элементы (r - 1) - ой строки, умноженные на . На ос­новании свойства 8 при таких преобразованиях мат­рицы ее определитель D не изменится, но так как r - я строка будет теперь состоять из одних нулей, то D = 0 - противоречие. Следовательно, наше предположение о том, что строки матрицы линейно зависимые, неверно.

Строки назовем базисными . Покажем, что любые (r+1) строк матрицы линейно зависимы, т.е. любая строка выражается через базисные.

Рассмотрим минор (r +1) - го порядка, который получается при дополнении рассматриваемого минора элементами еще одной строки i и столбца j . Этот минор равен нулю, так как ранг матрицы равен r , поэто­му любой минор более высокого порядка равен нулю.

Раскладывая его по элементам последнего (добавленного) столбца, получаем

Где модуль послед­него алгебраического дополнения совпадает с базисным мино­ром D и поэтому отлично от нуля, т.е. 0.

Система векторов одного и того же порядка называется линейно-зависимой, если из этих векторов путем соответствующей линейной комбинации можно получить нулевой вектор. (При этом не допускается, чтобы все коэффициенты линейной комбинации были равны нулю, так как это было бы тривиально.) В противном случае векторы называются линейно-независимыми. Например, следующие три вектора:

линейно зависимы, так как что легко проверить. В случае линейной зависимости любой вектор можно всегда выразить через линейную комбинацию остальных векторов. В нашем примере: или или Это легко проверить соответствующими расчетами. Отсюда вытекает следующее определение: вектор линейно независим от других векторов, если его нельзя представить в виде линейной комбинации из этих векторов.

Рассмотрим систему векторов, не уточняя, является ли она линейнозависимой или линейно-независимой. У каждой системы, состоящей из вектор-столбцов а, можно выявить максимально возможное число линейно-независимых векторов. Это число, обозначаемое буквой , и является рангом данной системы векторов. Так как каждую матрицу можно рассматривать как систему вектор-столбцов, ранг матрицы определяется как максимальное число содержащихся в ней линейнонезависимых вектор-столбцов. Для определения ранга матрицы пользуются и вектор-строками. Оба способа дают одинаковый результат для одной и той же матрицы, причем не может превосходить наименьшее из или Ранг квадратной матрицы порядка колеблется от 0 до . Если все векторы являются нулевыми, то ранг такой матрицы равен нулю. Если все векторы линейно независимы друг от друга, то ранг матрицы равен. Если образовать матрицу из приведенных выше векторов то ранг этой матрицы равен 2. Так как каждые два вектора могут быть сведены к третьему путем линейной комбинации, то ранг меньше 3.

Но можно убедиться, что любые два вектора из них являются-линейно-независимыми, следовательно, ранг

Квадратную матрицу называют вырожденной, если ее вектор-столбцы или вектор-строки линейно зависимы. Определитель такой матрицы равен нулю и обратной ей матрицы не существует, как уже было отмечено выше. Эти выводы эквивалентны друг другу. Вследствие этого квадратную матрицу называют невырожденной, или неособенной, если ее вектор-столбцы или вектор-строки независимы друг от друга. Определитель такой матрицы не равен нулю и обратная ей матрица существует (сравни со с. 43)

Ранг матрицы имеет вполне очевидную геометрическую интерпретацию. Если ранг матрицы равен , то говорят, что -мерное пространство натянуто на векторов. Если ранг то векторов лежат в -мерном подпространстве, которое всех их включает в себя. Итак, ранг матрицы соответствует минимально необходимой размерности пространства, «в котором содержатся все векторы», -мерное подпространство в -мерном пространстве называют -мерной гиперплоскостью. Ранг матрицы соответствует наименьшей размерности гиперплоскости, в которой еще лежат все векторы.

Ортогональность. Два вектора а и b называются взаимно-ортогональными, если их скалярное произведение равно нулю. Если для матрицы порядка имеет место равенство где D - диагональная матрица, то вектор-столбцы матрицы А попарно взаимно-ортогональны. Если эти вектор-столбцы пронормировать, т. е. привести к длине, равной 1, то имеет место равенство и говорят об ортонормированных векторах. Если В - квадратная матрица и имеет место равенство то матрицу В называют ортогональной. В этом случае из формулы (1.22) следует, что Ортогональная матрица всегда невырожденная. Отсюда из ортогональности матрицы следует линейная независимость ее вектор-строк или вектор-столбцов. Обратное утверждение неверно: из линейной независимости системы векторов не следует попарная ортогональность этих векторов.

Пусть в матрице А размеров (m; n) выбраны произвольно k строк и k столбцов (k ≤ min(m; n)). Элементы матрицы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором M kk порядка k y или минором k-го порядка матрицы A.

Рангом матрицы называется максимальный порядок r отличных от нуля миноров матрицы A, а любой минор порядка r, отличный от нуля, — базисным минором. Обозначение: rang A = r. Если rang A = rang B и размеры матриц A и Bсовпадают, то матрицы A и B называются эквивалентными. Обозначение: A ~ B.

Основными методами вычисления ранга матрицы являются метод окаймляющих миноров и метод .

Метод окаймляющих миноров

Суть метода окаймляющих миноров состоит в следующем. Пусть в матрице уже найден минор порядка k, отличный от нуля. Тогда далее рассматриваются лишь те миноры порядка k+1, которые содержат в себе (т. е. окаймляют) минорk-го порядка, отличный от нуля. Если все они равны нулю, то ранг матрицы равен k, в противном случае среди окаймляющих миноров (k+1)-го порядка найдется отличный от нуля и вся процедура повторяется.

Линейная независимость строк (столбцов) матрицы

Понятие ранга матрицы тесно связано с понятием линейной независимости ее строк (столбцов).

Строки матрицы :

называют линейно зависимыми, если найдутся такие числа λ 1 , λ 2 , λ k , что справедливо равенство:

Строки матрицы A называются линейно независимыми, если вышеприведённое равенство возможно лишь в случае, когда все числа λ 1 = λ 2 = … = λ k = 0

Аналогичным образом определяется линейная зависимость и независимость столбцов матрицы A.

Если какая-либо строка (a l) матрицы A (где (a l)=(a l1 , a l2 ,…, a ln)) может быть представлена в виде

Аналогичным образом определяется понятие линейной комбинации столбцов. Справедлива следующая теорема о базисном миноре.

Базисные строчки и базисные столбцы линейно независимы. Любая строка (либо столбец) матрицы A является линейной комбинацией базисных строк (столбцов), т. е. строк (столбцов), пересекающих базисный минор. Таким образом, ранг матрицы A: rang A = k равен максимальному числу линейно независимых строк (столбцов) матрицы A.

Т.е. ранг матрицы — это размерность самой большой квадратной матрицы внутри той матрицы, для которой нужно определить ранг, для которой определитель не равен нулю. Если исходная матрица не является квадратной, либо если она квадратная, но её определитель равен нулю, то для квадратных матриц меньшего порядка строки и столбцы выбираются произвольно.

Кроме как через определители, ранг матрицы можно посчитать по числу линейно независимых строк или столбцов матрицы. Он равен количеству линейно независимых строк или столбцов в зависимости от того, чего меньше. Например, если матрица имеет 3 линейно независимых строки и 5 линейно независимых столбцов, то её ранг равняется трём.

Примеры нахождения ранга матрицы

Методом окаймляющих миноров найти ранг матрицы

Р е ш е н и е. Минор второго порядка

окаймляющий минор M 2 , также отличен от нуля. Однако оба минора четвёртого порядка, окаймляющие M 3 .

равны нулю. Поэтому ранг матрицы A равен 3, а базисным минором является, например, представленный выше минор M 3 .

Метод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют её ранга. Используя эти преобразования, можно привести матрицу к виду, когда все её элементы, кроме a 11 , a 22 , …, a rr (r ≤min (m, n)), равны нулю. Это, очевидно, означает, что rang A = r. Заметим, что если матрица n-го порядка имеет вид верхней треугольной матрицы, т. е. матрицы, у которой все элементы под главной диагональю равны нулю, то её определитесь равен произведению элементов, стоящих на главной диагонали. Это свойство можно использовать при вычислении ранга матрицы методом элементарных преобразований: необходимо с их помощью привести матрицу к треугольной и тогда, выделив соответствующий определитель, найдём, что ранг матрицы равен числу элементов главной диагонали, отличных от нуля.

Методом элементарных преобразований найти ранг матрицы

Р е ш е н и е. Обозначим i-ю строку матрицы A символом α i . На первом этапе выполним элементарные преобразования

На втором этапе выполним преобразования

В результате получим

Каждую строку матрицы А обозначим е i = (a i 1 a i 2 …, a in) (например,
е 1 = (a 11 a 12 …, a 1 n), е 2 = (a 21 a 22 …, a 2 n) и т.д.). Каждая из них представляет собой матрицу-строку, которую можно умножить на число или сложить с другой строкой по общим правилам действий с матрицами.

Линейной комбинацией строк e l , e 2 ,...e k называют сумму произведений этих строк на произвольные действительные числа:
e = l l e l + l 2 e 2 +...+ l k e k , где l l , l 2 ,..., l k - произвольные числа (коэффициенты линейной комбинации).

Строки матрицы e l , e 2 ,...e m называются линейно зависимыми , если существуют такие числа l l , l 2 ,..., l m , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
l l e l + l 2 e 2 +...+ l m e m = 0, где 0 = (0 0...0).

Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных. Действительно, пусть для определенности последний коэффициент l m ¹ 0. Тогда, разделив обе части равенства на l m , получим выражение для последней строки, как линейной комбинации остальных строк:
e m = (l l /l m)e l + (l 2 /l m)e 2 +...+ (l m-1 /l m)e m-1 .

Если линейная комбинация строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю, т.е. l l e l + l 2 e 2 +...+ l m e m = 0 Û l k = 0 "k, то строки называют линейно независимыми .

Теорема о ранге матрицы . Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые можно линейно выразить все остальные ее строки или столбцы.

Докажем эту теорему. Пусть матрица А размера m х n имеет ранг r (r(А) £ min {m; n}). Следовательно, существует отличный от нуля минор r-го порядка. Всякий такой минор будем называть базисным . Пусть для определенности это минор

Строки этого минора также будем называть базисными .

Докажем, что тогда строки матрицы e l , e 2 ,...e r линейно независимы. Предположим противное, т.е. одна из этих строк, например r-я, является линейной комбинацией остальных: e r = l l e l + l 2 e 2 +...+ l r-1 e r-1 = 0. Тогда, если вычесть из элементов r-й строки элементы 1-й строки, умноженные на l l , элементы 2-й строки, умноженные на l 2 , и т.д., наконец, элементы (r-1)-й строки, умноженные на l r-1 , то r-я строка станет нулевой. При этом по свойствам определителя вышеприведенный определитель не должен измениться, и при этом должен быть равен нулю. Получено противоречие, линейная независимость строк доказана.

Теперь докажем, что любые (r+1) строк матрицы линейно зависимы, т.е. любую строку можно выразить через базисные.

Дополним рассмотренный ранее минор еще одной строкой (i-й) и еще одним столбцом (j-м). В результате получим минор (r+1)-го порядка, который по определению ранга равен нулю.