Лабораторная работа №6. Проверка гипотезы о нормальном распределении выборки по критерию Пирсона.

Лабораторная работа выполняется в Excel 2007.

Цель работы – дать навыки первичной обработки данных, построении гистограмм, подборе подходящего закона распределения и вычислении его параметров, проверка согласия между эмпирическим и гипотетическим законом распределения по критерию хи-квадрат Пирсона средствами Excel.

1. Формирование выборки нормально распределенных случайных чисел с заданными значениями математического ожидания и среднего квадратического отклонения.

Данные → Анализ данных → Генерация случайных чисел → ОК .

Рис. 1. Диалоговое окно Анализ данных

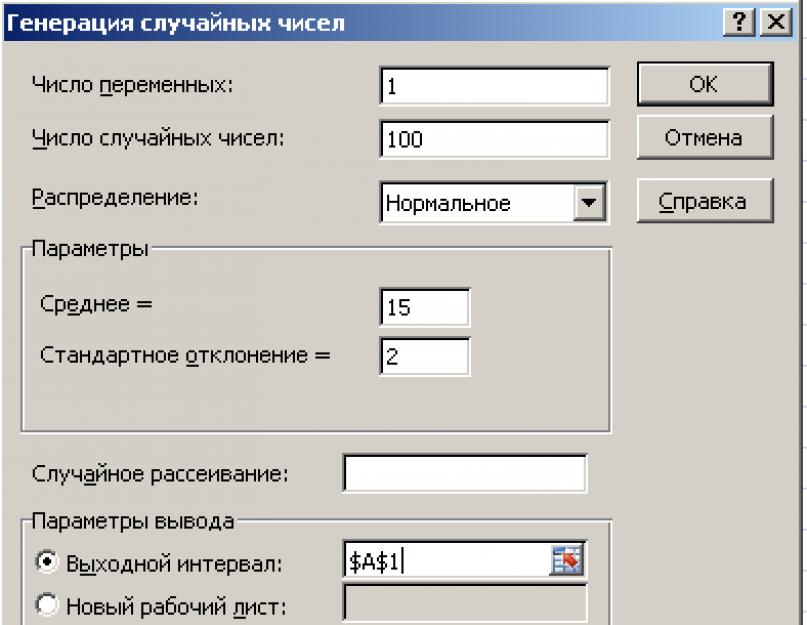
В появившемся окне Генерация случайных чисел ввести:

Число переменных: 1 ;

Число случайных чисел: 100 ;

Распределение: Нормальное .

Параметры:

Среднее = 15 (математическое ожидание);

Стандартное отклонение = 2 (среднее квадратическое отклонение);

Случайное рассеивание: не заполнять (или заполнить по указанию преподавателя );

Выходной интервал: адрес первой ячейки столбца массива случайных чисел - $ A $1 . ОК .

Рис. 2. Диалоговое окно Генерация случайных чисел с заполненными полями ввода

В результате выполнения операции Генерация случайных чисел появится столбец $ A $1: $A$100 , содержащий 100 случайных чисел.

Рис. 3. Фрагмент листа Excel первых нескольких случайных чисел $A$1: $A$100.

2. Определение параметров выборки, описательные статистики

В главном меню Excel выбрать: Данные → Анализ данных → Описательная статистика → ОК .

В появившемся окне Описательная статистика ввести:

Входной интервал – 100 случайных чисел в ячейках $ A $1: $ A $100 ;

Группирование - по столбцам;

Выходной интервал – адрес ячейки, с которой начинается таблица Описательная статистика - $ C $1 ;

Итоговая статистика – поставить галочку. ОК.

Рис. 4. Диалоговое окно Описательная статистика с заполненными полями ввода.

На листе Excel появится таблица – Столбец 1

Рис. 5. Таблица Столбец 1 с данными процедуры Описательная статистика .

Таблица содержит описательные статистики, в частности:

Среднее – оценка математического ожидания;

Стандартное отклонение – оценка среднего квадратического отклонения;

Эксцесс и Асимметричность – оценки эксцесса и асимметрии.

Приблизительное равенство нулю оценок эксцесса и асимметрии, и приблизительное равенство оценки среднего оценке медианы дает предварительное основание выбрать в качестве основной гипотезы H 0 распределения элементов генеральной совокупности - нормальный закон.

Интервал – размах выборки;

Минимум – минимальное значение случайной величины в выборке;

Максимум – максимальное значение случайной величины в выборке.

В ячейке F 15 - длина частичного интервала h , вычисленная следующим образом:

Число интервалов группировки k в Excel вычисляется автоматически по формуле

где, скобки означают – округление до целой части числа в меньшую сторону.

В рассматриваемом варианте n = 100 , следовательно, k = 11 . Действительно:

Эта формула занесена в ячейку F 15: =($D$13-$D$12)/10

Результаты процедуры Описательная статистика потребуются в дальнейшем при построении теоретического закона распределения.

Задача 1.

Используя критерий Пирсона, при уровне значимости a = 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.

Решение.

1. Вычислим и выборочное среднее квадратическое отклонение .
2. Вычислим теоретические частоты учитывая, что n = 200, h = 2, = 4,695, по формуле
.

Составим расчетную таблицу (значения функции j (x ) приведены в приложении 1).

i

3. Сравним эмпирические и теоретические частоты. Составим расчетную таблицу, из которой найдем наблюдаемое значение критерия :

i
Сумма

По таблице критических точек распределения (приложение 6), по уровню значимости a = 0,05 и числу степеней свободы k = s – 3 = 9 – 3 = 6 находим критическую точку правосторонней критической области (0,05; 6) = 12,6.
Так как =22,2 > = 12,6, гипотезу о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические и теоретические частоты различаются значимо.

Задача2

Представлены статистические данные.

Результаты измерений диаметров n = 200 валков после шлифовки обобщены в табл. (мм):
Таблица Частотный вариационный ряд диаметров валков

i
xi , мм

xi , мм

Требуется:

1) составить дискретный вариационный ряд, при необходимости упорядочив его;

2) определить основные числовые характеристики ряда;

3) дать графическое представление ряда в виде полигона (гистограммы) распределения;

4) построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона. При проверке статистической гипотезы о виде распределения принять уровень значимости a = 0,05

Решение: Основные числовые характеристики данного вариационного ряда найдем по определению. Средний диаметр валков равен (мм):
x ср = = 6,753;
исправленная дисперсия (мм2):
D = = 0,0009166;
исправленное среднее квадратическое (стандартное) отклонение (мм):
s = = 0,03028.


Рис. Частотное распределение диаметров валков

Исходное («сырое») частотное распределение вариационного ряда, т.е. соответствие ni (xi ), отличается довольное большим разбросом значений ni относительно некоторой гипотетической «усредняющей» кривой (рис.). В этом случае предпочтительно построить и анализировать интервальный вариационный ряд, объединяя частоты для диаметров, попадающих в соответствующие интервалы.
Число интервальных групп K определим по формуле Стерджесса:
K = 1 + log2n = 1 + 3,322lgn ,
где n = 200 – объем выборки. В нашем случае
K = 1 + 3,322×lg200 = 1 + 3,322×2,301 = 8,644 » 8.
Ширина интервала равна (6,83 – 6,68)/8 = 0,01875 » 0,02 мм.
Интервальный вариационный ряд представлен в табл.

Таблица Частотный интервальный вариационный ряд диаметров валков.

k
xk , мм

Интервальный ряд может быть наглядно представлен в виде гистограммы частотного распределения.


Рис . Частотное распределение диаметров валков. Сплошная линия – сглаживающая нормальная кривая.

Вид гистограммы позволяет сделать предположение о том, что распределение диаметров валков подчиняется нормальному закону, согласно которому теоретические частоты могут быть найдены как
nk , теор = n ×N (a ; s; xk )×Dxk ,
где, в свою очередь, сглаживающая гауссова кривая нормального распределения определяется выражением:
N (a ; s; xk ) = .
В этих выражениях xk – центры интервалов в частотном интервальном вариационном ряде.

Например, x 1 = (6,68 + 6,70)/2 = 6,69. В качестве оценок центра a и параметра s гауссовой кривой можно принять:
a = x ср.
Из рис. видно, что гауссова кривая нормального распределения в целом соответствует эмпирическому интервальному распределению. Однако следует удостовериться в статистической значимости этого соответствия. Используем для проверки соответствия эмпирического распределения эмпирическому критерий согласия Пирсона c2 . Для этого следует вычислить эмпирическое значение критерия как сумму
= ,
где nk и nk ,теор – эмпирические и теоретические (нормальные) частоты, соответственно. Результаты расчетов удобно представить в табличном виде:
Таблица Вычисления критерия Пирсона

[xk , xk+ 1), мм	xk , мм		nk ,теор

Критическое значение критерия найдем по таблице Пирсона для уровня значимости a = 0,05 и числа степеней свободы d .f . = K – 1 – r , где K = 8 – число интервалов интервального вариационного ряда; r = 2 – число параметров теоретического распределения, оцененных на основании данных выборки (в данном случае, – параметры a и s). Таким образом, d .f . = 5. Критическое значение критерия Пирсона есть крит(a; d .f .) = 11,1. Так как c2эмп < c2крит, заключаем, что согласие между эмпирическим и теоретическим нормальным распределением является статистическим значимым. Иными словами, теоретическое нормальное распределение удовлетворительно описывает эмпирические данные.

Задача3

Коробки с шоколадом упаковываются автоматически. По схеме собственно-случайной бесповторной выборки взято 130 из 2000 упаковок, содержащихся в партии, и получены следующие данные об их весе:

Требуется используя критерий Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X – вес упаковок – распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.

Решение

1012,5
= 615,3846

Примечание:

В принципе в качестве дисперсии нормального закона распределения следует взять исправленную выборочную дисперсию. Но т.к. количество наблюдений – 130 достаточно велико, то подойдет и “обычная” .
Таким образом, теоретическое нормальное распределение имеет вид:

Интервал

[xi ; xi+1 ]

Эмпирические частоты

ni

Вероятности
pi

Теоретические частоты
npi

(ni-npi)2

​ Критерий χ 2 Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).

1. История разработки критерия χ 2

Критерий хи-квадрат для анализа таблиц сопряженности был разработан и предложен в 1900 году английским математиком, статистиком, биологом и философом, основателем математической статистики и одним из основоположников биометрики Карлом Пирсоном (1857-1936).

2. Для чего используется критерий χ 2 Пирсона?

Критерий хи-квадрат может применяться при анализе таблиц сопряженности , содержащих сведения о частоте исходов в зависимости от наличия фактора риска. Например, четырехпольная таблица сопряженности выглядит следующим образом:

	Исход есть (1)	Исхода нет (0)	Всего
Фактор риска есть (1)	A	B	A + B
Фактор риска отсутствует (0)	C	D	C + D
Всего	A + C	B + D	A + B + C + D

Как заполнить такую таблицу сопряженности? Рассмотрим небольшой пример.

Проводится исследование влияния курения на риск развития артериальной гипертонии. Для этого были отобраны две группы исследуемых - в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую - 80 некурящих такого же возраста. В первой группе у 40 человек отмечалось повышенное артериальное давление. Во второй - артериальная гипертония наблюдалась у 32 человек. Соответственно, нормальное артериальное давление в группе курильщиков было у 30 человек (70 - 40 = 30) а в группе некурящих - у 48 (80 - 32 = 48).

Заполняем исходными данными четырехпольную таблицу сопряженности:

В полученной таблице сопряженности каждая строчка соответствует определенной группе исследуемых. Столбцы - показывают число лиц с артериальной гипертонией или с нормальным артериальным давлением.

Задача, которая ставится перед исследователем: имеются ли статистически значимые различия между частотой лиц с артериальным давлением среди курящих и некурящих? Ответить на этот вопрос можно, рассчитав критерий хи-квадрат Пирсона и сравнив получившееся значение с критическим.

3. Условия и ограничения применения критерия хи-квадрат Пирсона

1. Сопоставляемые показатели должны быть измерены в номинальной шкале (например, пол пациента - мужской или женский) или в порядковой (например, степень артериальной гипертензии, принимающая значения от 0 до 3).
2. Данный метод позволяет проводить анализ не только четырехпольных таблиц, когда и фактор, и исход являются бинарными переменными, то есть имеют только два возможных значения (например, мужской или женский пол, наличие или отсутствие определенного заболевания в анамнезе...). Критерий хи-квадрат Пирсона может применяться и в случае анализа многопольных таблиц, когда фактор и (или) исход принимают три и более значений.
3. Сопоставляемые группы должны быть независимыми, то есть критерий хи-квадрат не должен применяться при сравнении наблюдений "до-"после". В этих случаях проводится тест Мак-Немара (при сравнении двух связанных совокупностей) или рассчитывается Q-критерий Кохрена (в случае сравнения трех и более групп).
4. При анализе четырехпольных таблиц ожидаемые значения в каждой из ячеек должны быть не менее 10. В том случае, если хотя бы в одной ячейке ожидаемое явление принимает значение от 5 до 9, критерий хи-квадрат должен рассчитываться с поправкой Йейтса . Если хотя бы в одной ячейке ожидаемое явление меньше 5, то для анализа должен использоваться точный критерий Фишера .
5. В случае анализа многопольных таблиц ожидаемое число наблюдений не должно принимать значения менее 5 более чем в 20% ячеек.

4. Как рассчитать критерий хи-квадрат Пирсона?

Для расчета критерия хи-квадрат необходимо:

Данный алгоритм применим как для четырехпольных, так и для многопольных таблиц.

5. Как интерпретировать значение критерия хи-квадрат Пирсона?

В том случае, если полученное значение критерия χ 2 больше критического, делаем вывод о наличии статистической взаимосвязи между изучаемым фактором риска и исходом при соответствующем уровне значимости.

6. Пример расчета критерия хи-квадрат Пирсона

Определим статистическую значимость влияния фактора курения на частоту случаев артериальной гипертонии по рассмотренной выше таблице:

1. Рассчитываем ожидаемые значения для каждой ячейки:
2. Находим значение критерия хи-квадрат Пирсона:

   χ 2 = (40-33.6) 2 /33.6 + (30-36.4) 2 /36.4 + (32-38.4) 2 /38.4 + (48-41.6) 2 /41.6 = 4.396.

3. Число степеней свободы f = (2-1)*(2-1) = 1. Находим по таблице критическое значение критерия хи-квадрат Пирсона, которое при уровне значимости p=0.05 и числе степеней свободы 1 составляет 3.841.
4. Сравниваем полученное значение критерия хи-квадрат с критическим: 4.396 > 3.841, следовательно зависимость частоты случаев артериальной гипертонии от наличия курения - статистически значима. Уровень значимости данной взаимосвязи соответствует p<0.05.

1.Открыть программу Excel

2.Создать столбцы с данными. В нашем примере мы будем считать взаимосвязь, или корреляцию, между агрессивностью и неуверенностью в себе у детей-первоклассников. В эксперименте участвовали 30 детей, данные представлены в таблице эксель:

1 столбик — № испытуемого

2 столбик — агрессивность в баллах

3 столбик — неуверенность в себе в баллах

3.Затем необходимо выбрать пустую ячейку рядом с таблицей и нажать на значок f(x) в панели Excel

4.Откроется меню функций, среди категорий необходимо выбрать Статистические , а затем среди списка функций по алфавиту найти КОРРЕЛ и нажать ОК

5.Затем откроется меню аргументов функции, которое позволит выбрать нужные нам столбики с данными. Для выбора первого столбика Агрессивность нужно нажать на синюю кнопочку у строки Массив1

6.Выберем данные для Массива1 из столбика Агрессивность и нажмем на синюю кнопочку в диалоговом окне

7. Затем аналогично Массиву 1 нажмём на синюю кнопочку у строки Массив2

8.Выберем данные для Массива2 — столбик Неуверенность в себе и опять нажмем синюю кнопку, затем ОК

9.Вот, коэффициент корреляции r-Пирсона посчитан и записан в выбранной ячейке.В нашем случае он положительный и приблизительно равен 0,225 . Это говорит об умеренной положительной связи между агрессивностью и неуверенностью в себе у детей-первоклассников

Таким образом, статистическим выводом эксперимента будет: r = 0,225, выявлена умеренная положительная взаимосвязь между переменными агрессивность и неуверенность в себе.

В некоторых исследованиях требуется указывать р-уровень значимости коэффициента корреляции, однако программа Excel, в отличие от SPSS, не предоставляет такой возможности. Ничего страшного, есть (А.Д. Наследов).

Также Вы можете и приложить её к результатам исследования.

Оценка соответствия нормальному распределению

Этот метод используется для проверки согласия опытного и теоретического распределения, если число испытаний больше 100.

Суть метода заключается в определении критерия Пирсона (c 2 ) с последующим сравнением полученного значения с теоретическим.

Порядок определения критерия Пирсона:

Определяют среднее значение и среднее квадратическое отклонение. Для расчета критерия Пирсона составляют таблицу (таблице 11).

2. Определяют отношение

3. С помощью специальной таблицы (таблица 12) определяют частоту распределения Y 0 .

Таблица 11

Таблица 12

t	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9	0,3989 0,2420 0,0544 0,0044

4. Рассчитывают теоретическое значение частот

(40)

где n - общее число испытаний;

k - классовый интервал;

S - среднее квадратическое отклонение.

5. Определяют разность между фактической и теоретической частотой распределения

y i – U т (41)

рассчитывают

6. Находят критерий Пирсона

(43)

7. Определяют число степеней свободы

С = m-3 (44)

где C - число степеней свободы;

m - число классов или строк.

8. Задаваясь доверительной вероятностью q , определяют теоретическое значение критерия Пирсона.

9. Сравнивают c ф 2 с c т 2. Если c 2 ф < c 2 т , то для принятой доверительной вероятности гипотеза о согласии опытного и теоретического распределения принимается, в противном случае отвергается.

В программе Excel проверка осуществляется с помощью функции ХИ2ТЕСТ (рис. 22). ХИ2ТЕСТ возвращает значение для распределения χ 2 Критерий используется для определения того, подтверждается ли гипотеза экспериментом.

Рис. 22. Функция ХИ2ТЕСТ

ХИ2ТЕСТ (фактический_интервал ;ожидаемый_интервал )

Фактический_интервал - это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями.

Ожидаемый_интервал - это интервал данных, который содержит отношение произведений итогов по строкам и столбцам к общему итогу.

Если фактический_интервал и ожидаемый_интервал имеют различное количество точек данных, то функция ХИ2ТЕСТ возвращает значение ошибки #Н/Д.

Критерий χ 2 сначала вычисляет χ 2 статистику, используя формулу:

(45)

где A ij - фактическая частота в i -ой строке, j -ом столбце

E ij - ожидаемая частота в i-ой строке, j-ом столбце

r - число строк

c - число столбцов

Значение критерия χ 2 является индикатором независимости. Как видно из формулы, критерий χ 2 всегда положительный или равен 0, а последнее возможно только, если A ij = E ij при любых значениях i,j .

ХИ2ТЕСТ возвращает вероятность того, что при условии независимости может быть получено значение χ 2 статистики по крайней мере такое же высокое, как полученное из приведенной выше формулы. Чтобы вычислить эту вероятность, ХИ2ТЕСТ использует распределение χ 2 с соответствующим числом степеней свободы (df ). Если r > 1, а c > 1, то df = (r - 1)(c - 1). Если r = 1, а c > 1, то df = c - 1 или если r > 1, а c = 1, то df = r - 1. Равенство, где r = c= 1, не позволительно, поэтому появится сообщение об ошибке #Н/Д.

Функцию ХИ2ТЕСТ можно использовать в тех случаях, когда гипотетическое распределение задано полностью, то есть заданы не только вид гипотетического закона распределения, но и все параметры этого закона. Только в этом случае функция правильно выдает число степеней свободы.

ХИ2РАСП (x;степени_свободы) (рис. 23) возвращает одностороннюю вероятность распределения хи-квадрат. Распределение χ 2 связано с критерием χ 2 . Критерий χ 2 используется для сравнения предполагаемых и наблюдаемых значений. Например, в генетическом эксперименте выдвигается гипотеза, что следующее поколение растений будет обладать определенной окраской. Сравнивая наблюдаемые результаты с предполагаемыми, можно определить, была ли верна исходная гипотеза.

х – значение, для которого требуется вычислить распределение.

Степени_свободы – число степеней свободы.

Рис. 23. Функция ХИ2РАСП

Если какой-либо из аргументов не является числом, функция ХИ2РАСП возвращает значение ошибки #ЗНАЧ!.

Если x отрицательное значение, функция ХИ2РАСП

Если степени_свободы < 1 или степени_свободы > 10^10, функция ХИ2РАСП возвращает значение ошибки #ЧИСЛО!.

ХИ2РАСП вычисляется как ХИ2РАСП = P(X> x), где x - χ 2 случайная величина.

ХИ2ОБР (вероятность;степени_свободы) (рис. 24) возвращает значение, обратное односторонней вероятности распределения хи-квадрат. Если вероятность = ХИ2РАСП (x;...), то ХИ2ОБР (вероятность;...) = x. Данная функция позволяет сравнить наблюдаемые результаты с ожидаемыми, чтобы определить, была ли верна исходная гипотеза.

Вероятность - вероятность, связанная с распределением c2 (хи-квадрат).

Степени_свободы - число степеней свободы.

Если какой-либо из аргументов не является числом, функция ХИ2ОБР возвращает значение ошибки #ЗНАЧ!

Рис. 24. Функция ХИ2ОБР

Если вероятность < 0 или вероятность > 1, функция ХИ2ОБР возвращает значение ошибки #ЧИСЛО!

Если значение аргумента «степени_свободы» не является целым числом, оно усекается.

Если степени_свободы < 1 или степени_свободы ≥ 10^10, ХИ2ОБР возвращает значение ошибки #ЧИСЛО!

Если задано значение вероятности, то функция ХИ2ОБР ищет значение x, для которого функция ХИ2РАСП (x; степень_свободы) = вероятность. Однако точность функции ХИ2ОБР зависит от точности ХИ2РАСП . В функции ХИ2ОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает сообщение об ошибке #Н/Д.