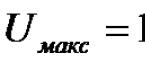Смысл спектрального анализа сигналов заключается в изучении того, как сигнал может быть представлен в виде суммы (или интеграла) простых гармонических колебаний и как форма сигнала определяет структуру распределения по частотам амплитуд и фаз этих колебаний. В противоположность этому задачей корреляционного анализа сигналов является определение меры степени сходства и различия сигналов или сдвинутых по времени копий одного сигнала. Введение меры открывает пути к проведению количественных измерений степени схожести сигналов. Будет показано, что существует определенная взаимосвязь между спектральными и корреляционными характеристиками сигналов.

3.1 Автокорреляционная функция (акф)

Автокорреляционная функция сигнала с конечной энергией – это значение интеграла от произведения двух копий этого сигнала, сдвинутых относительно друг друга на время τ, рассматриваемое в функции этого временного сдвига τ:

Если сигнал определен на конечном интервале времени , то его АКФ находится как:

где
- интервал перекрытия сдвинутых копий сигнала.

Считается, что чем больше значение автокорреляционной функции
при данном значении, тем в большей степени две копии сигнала, сдвинутые на промежуток времени, похожи друг на друга. Поэтому корреляционная функция
и является мерой сходства для сдвинутых копий сигнала.

Вводимая таким образом мера сходства для сигналов, имеющих форму случайных колебаний вокруг нулевого значения, обладает следующими характерными свойствами.

Если сдвинутые копии сигнала колеблются примерно в такт друг к другу, то это является признаком их схожести и АКФ принимает большие положительные значения (большая положительная корреляция). Если копии колеблются почти в противофазе, АКФ принимает большие отрицательные значения (антисходство копий сигнала, большая отрицательная корреляция).

Максимум АКФ достигается при совпадении копий, то есть при отсутствии сдвига. Нулевые значения АКФ достигаются при сдвигах, при которых не заметно ни сходства, ни антисходства копий сигнала (нулевая корреляция, отсутствие корреляции).

На рис.3.1 изображен фрагмент реализации некоторого сигнала на интервале времени от 0 до 1 с. Сигнал случайным образом колеблется вокруг нулевого значения. Поскольку интервал существования сигнала конечен, то конечна и его энергия. Его АКФ можно вычислить в соответствии с уравнением:

Автокорреляционная функция сигнала, вычисленная вMathCad в соответствии с этим уравнением, представлена на рис. 3.2. Корреляционная функция показывает не только то, что сигнал похож сам на себя (сдвиг τ=0), но и то, что некоторой схожестью обладают и копии сигнала, сдвинутые друг относительно друга приблизительно на 0.063 с (боковой максимум автокорреляционной функции). В противоположность этому копии сигнала сдвинутые на 0.032 с, должны быть антипохожи дуг на друга, то есть быть в некотором смысле противоположными друг другу.

На рис.33 показаны пары этих двух копий. По рисунку можно проследить, что понимается под похожестью и антипохожестью копий сигнала.

Корреляционная функция обладает следующими свойствами:

1. При τ = 0 автокорреляционная функция принимает наибольшее значение, равное энергии сигнала

2. Автокорреляционная функция является четной функцией временного сдвига
.

3. С ростом τ автокорреляционная функция убывает до нуля

4. Если сигнал не содержит разрывов типа δ - функций, то
- непрерывная функция.

5. Если сигнал является электрическим напряжением, то корреляционная функция имеет размерность
.

Для периодических сигналов в определении автокорреляционной функции тот же самый интеграл делят еще на период повторения сигнала:

Так введенная корреляционная функция отличается следующими свойствами:

Для примера вычислим корреляционную функцию гармонического колебания :

Используя ряд тригонометрических преобразований, получим окончательно:

Таким образом, автокорреляционная функция гармонического колебания является косинусоидой с тем же периодом изменения, что и сам сигнал. При сдвигах, кратных периоду колебания, гармоника преобразуется в себя и АКФ принимает наибольшие значения, равные половине квадрата амплитуды. Сдвиги по времени, кратные половине периода колебания, равносильны смещению фазы на угол
, при этом меняется знак колебаний, а АКФ принимает минимальное значение, отрицательное и равное половине квадрата амплитуды. Сдвиги, кратные четверти периода, переводят, например, синусоидальное колебание в косинусоидальное и наоборот. При этом АКФ обращается в нуль. Такие сигналы, находящиеся в квадратуре друг относительно друга, с точки зрения автокорреляционной функции оказываются совершенно не похожими друг на друга.

Важным является то, что в выражение для корреляционной функции сигнала не вошла его начальная фаза. Информация о фазе потерялась. Это означает, что по корреляционной функции сигнала нельзя восстановить сам сигнал. Отображение
в противоположность отображению
не является взаимно однозначным.

Если под механизмом генерирования сигналов понимать некоего демиурга, создающего сигнал по выбранной им корреляционной функции, то он смог бы создать целую совокупность сигналов (ансамбль сигналов), имеющих действительно одну и ту же корреляционную функцию, но отличающихся друг от друга фазовыми соотношениями.

актом проявления сигналом своей свободной воли, независимой от воли создателя (возникновение отдельных реализаций некоторого случайного процесса),

результатом постороннего насилия над сигналом (введение в сигнал измерительной информации, получаемой при проведении измерений какой либо физической величины).

Аналогичным образом обстоит дело с любым периодическим сигналом. Если периодический сигнал с основным периодом Т имеет амплитудный спектр
и фазовый спектр
, то корреляционная функция сигнала принимает следующий вид:

Уже в этих примерах проявляется некоторая связь между корреляционной функцией и спектральными свойствами сигнала. Подробнее об этих соотношениях речь пойдет в дальнейшем.

Signals and linear systems. Correlation of signals

Тема 6. Корреляция сигналов

Предельный страх и предельный пыл храбрости одинаково расстраивают желудок и вызывают понос.

Мишель Монтень. Французский юрист-мыслитель, XVI в.

Вот это номер! Две функции имеют стопроцентную корреляцию с третьей и ортогональны друг другу. Ну и шуточки были у Всевышнего при сотворении Мира.

Анатолий Пышминцев. Новосибирский геофизик Уральской школы, ХХ в.

1. Автокорреляционные функции сигналов. Понятие автокорреляционных функций (АКФ). АКФ сигналов, ограниченных во времени. АКФ периодических сигналов. Функции автоковариации (ФАК). АКФ дискретных сигналов. АКФ зашумленных сигналов. АКФ кодовых сигналов.

2. Взаимнокорреляционные функции сигналов (ВКФ). Взаимная корреляционная функция (ВКФ). Взаимная корреляция зашумленных сигналов. ВКФ дискретных сигналов.Оценка периодических сигналов в шуме. Функция взаимных корреляционных коэффициентов.

3. Спектральные плотности корреляционных функций. Спектральная плотность АКФ. Интервал корреляции сигнала. Спектральная плотность ВКФ. Вычисление корреляционных функций при помощи БПФ.

Введение

Корреляция (correlation), и ее частный случай для центрированных сигналов – ковариация, является методом анализа сигналов. Приведем один из вариантов использования метода. Допустим, что имеется сигнал s(t), в котором может быть (а может и не быть) некоторая последовательность x(t) конечной длины Т, временное положение которой нас интересует. Для поиска этой последовательности в скользящем по сигналу s(t) временном окне длиной Т вычисляются скалярные произведения сигналов s(t) и x(t). Тем самым мы "прикладываем" искомый сигнал x(t) к сигналу s(t), скользя по его аргументу, и по величине скалярного произведения оцениваем степень сходства сигналов в точках сравнения.

Корреляционный анализ дает возможность установить в сигналах (или в рядах цифровых данных сигналов) наличие определенной связи изменения значений сигналов по независимой переменной, то есть, когда большие значения одного сигнала (относительно средних значений сигнала) связаны с большими значениями другого сигнала (положительная корреляция), или, наоборот, малые значения одного сигнала связаны с большими значениями другого (отрицательная корреляция), или данные двух сигналов никак не связаны (нулевая корреляция).

В функциональном пространстве сигналов эта степень связи может выражаться в нормированных единицах коэффициента корреляции, т.е. в косинусе угла между векторами сигналов, и, соответственно, будет принимать значения от 1 (полное совпадение сигналов) до -1 (полная противоположность) и не зависит от значения (масштаба) единиц измерений.

В варианте автокорреляции (autocorrelation) по аналогичной методике производится определение скалярного произведения сигнала s(t) с собственной копией, скользящей по аргументу. Автокорреляция позволяет оценить среднестатистическую зависимость текущих отсчетов сигнала от своих предыдущих и последующих значений (так называемый радиус корреляции значений сигнала), а также выявить в сигнале наличие периодически повторяющихся элементов.

Особое значение методы корреляции имеют при анализе случайных процессов для выявления неслучайных составляющих и оценки неслучайных параметров этих процессов.

Заметим, что в терминах "корреляция" и "ковариация" существует некоторая путаница. В математической литературе термин "ковариация" применяется к центрированным функциям, а "корреляция" – к произвольным. В технической литературе, и особенно в литературе по сигналам и методам их обработки, часто применяется прямо противоположная терминология. Принципиального значения это не имеет, но при знакомстве с литературными источниками стоит обращать внимание на принятое назначение данных терминов.

Литература: [Л.1], с 77-83

[Л.2], с 22-26

[Л.3], с 39-43

Во многих радиотехнических задачах часто возникает необходимость сравнения сигнала и его копии, сдвинутой на некоторое время

При снятии АКФ на один из входов перемножителя поступает сигнал , а на второй – этот же сигнал, но задержанный на время . Сигнал, пропорциональный произведению , подвергается операции интегрирования. На выходе интегратора формируется напряжение, пропорциональное значению АКФ при фиксированном . Изменяя время задержки, можно построить АКФ сигнала.

Для экспериментального построения ВКФ сигнал подается на один из входов перемножителя, а сигнал – на устройство задержки (входящие цепи показаны пунктиром). В остальном, устройство работает аналогичным образом. Отметим, что описанное устройство называется коррелятором и широко используется в различных радиотехнических системах для приема и обработки сигналов.

До сих пор мы проводили корреляционный анализ непериодических сигналов, обладающих конечной энергией. Вместе с тем, необходимость подобного анализа часто возникает и для периодических сигналов, которые теоретически обладают бесконечной энергией, но конечной средней мощностью. В этом случае АКФ и ВКФ вычисляются усреднением по периоду и имеют смысл средней мощности (собственной или взаимной соответственно). Таким образом, АКФ периодического сигнала:

, (2.66)

а взаимная корреляционная функция двух периодических сигналов с кратными периодами:

, (2.67)

где – наибольшее значение периода.

Найдем автокорреляционную функцию гармонического сигнала

где – круговая частота, – начальная фаза.

Подставляя это выражение в (2.66) и вычисляя интеграл с использованием известного тригонометрического соотношения:

Из рассмотренного примера можно сделать следующие выводы, справедливые для любого периодического сигнала.

1. АКФ периодического сигнала является периодической функцией с тем же периодом.

2. АКФ периодического сигнала является четной функцией аргумента .

3. При значение представляет собой среднюю мощность, которая выделяется на сопротивлении в 1 Ом и имеет размеренность .

4. АКФ периодического сигнала не содержит информации о начальной фазе сигнала.

Следует также отметить, что интервал корреляции периодического сигнала .

А теперь вычислим взаимную корреляционную функцию двух гармонических сигналов одинаковой частоты, но отличающихся амплитудами и начальными фазами

и .

Воспользовавшись (2.67) и проводя несложные вычисления, получим

где – разность начальных фаз сигналов и .

Таким образом, взаимная корреляционная функция двух рассматриваемых сигналов содержит информацию о разности начальных фаз. Это важное свойство широко используется при построении различных радиотехнических устройств, в частности, устройств синхронизации некоторых систем радиоавтоматики и других.

В заключение установим связь между АКФ непериодического сигнала и его энергетическим спектром, определение которого [см. (2.51)] было дано выше. Для этого воспользуемся (2.49) при . Тогда получим соотношение

где – функция, комплексно сопряженная с .

Положим теперь и . В соответствии с (2.45) преобразование Фурье имеет вид

С другой стороны

Подставляя эти выражения в (2.68), получим

Но в соответствие с (2.51) есть энергетический спектр. Тогда окончательно

. (2.69)

Применяя к прямое преобразование Фурье, приходим к соотношению

. (2.70)

Таким образом, АКФ и энергетический спектр сигнала связаны парой преобразований Фурье.

Так как и – вещественные и четные функции, выражения (2.69) и (2.70) можно записать соответственно в виде

, (2.71)

. (2.72)

Рассмотренный корреляционно-спектральный анализ позволяет дать еще одну трактовку эффективной ширины спектра. Если известен энергетический спектр, то эффективная ширина спектра определяется так:

. (2.73)

Иными словами представляет собой сторону прямоугольника по площади равного площади под кривой одностороннего спектра, вторая сторона которого равна (рис.2.13). Очевидно, произведение эффективной ширины энергетического спектра на величину интервала корреляции есть величина постоянная

Таким образом, и в этом случае мы сталкиваемся с проявлением принципа неопределенности: чем больше интервал корреляции, тем меньше ширина энергетического спектра, и наоборот.

Контрольные вопросы к главе 2

1. Что такое система базисных тригонометрических функций?

2. Как можно записать тригонометрический ряд Фурье?

3. Дайте определение амплитудного и фазового спектра периодического сигнала.

4. Какой характер носит спектр последовательности прямоугольных импульсов?

5. Чем отличается спектр одиночного импульса от спектра периодической последовательности импульсов?

6. Запишите прямое и обратное преобразование Фурье.

7. Как найти эффективную длительность и эффективную ширину спектра прямоугольного сигнала?

8. Что представляет собой спектр сигнала в виде дельта-функции?

9. Дайте определение автокорреляционной функции детерминированного сигнала.

10. Что такое взаимная корреляционная функция двух сигналов?

11. Как найти коэффициент взаимной корреляции?

12. Какими свойствами обладает автокорреляционная функция периодического сигнала?

Функции корреляции сигналов применяются для интегральных количественных оценок формы сигналов и степени их сходства друг с другом.

Автокорреляционные функции (АКФ) сигналов (correlation function, CF). Применительно к детерминированным сигналам с конечной энергией АКФ является количественной интегральной характеристикой формы сигнала, и представляет собой интеграл от произведения двух копий сигнала s(t), сдвинутых относительно друг друга на время t:

B s (t) = s(t) s(t+t) dt. (2.25)

Как следует из этого выражения, АКФ является скалярным произведением сигнала и его копии в функциональной зависимости от переменной величины значения сдвига t. Соответственно, АКФ имеет физическую размерность энергии, а при t = 0 значение АКФ непосредственно равно энергии сигнала:

B s (0) =s(t) 2 dt = E s .

Функция АКФ является непрерывной и четной. В последнем нетрудно убедиться заменой переменной t = t-t в выражении (2.25):

B s (t) =s(t-t) s(t) dt = s(t) s(t-t) dt = B s (-t). (2.25")

С учетом четности, графическое представление АКФ производится только для положительных значений t. На практике сигналы обычно задаются на интервале положительных значений аргументов от 0-Т. Знак +t в выражении (2.25) означает, что при увеличении значений t копия сигнала s(t+t) сдвигается влево по оси t и уходит за 0, что требует соответствующего продления сигнала в область отрицательных значений аргумента. А так как при вычислениях интервал задания t, как правило, много меньше интервала задания сигнала, то более практичным является сдвиг копии сигнала влево по оси аргументов, т.е. применение в выражении (2.25) функции s(t-t) вместо s(t+t).

По мере увеличения значения величины сдвига t для финитных сигналов временное перекрытие сигнала с его копией уменьшается и скалярное произведение стремятся к нулю.

Пример. На интервале (0,Т) задан прямоугольный импульс с амплитудным значением, равным А. Вычислить автокорреляционную функцию импульса.

При сдвиге копии импульса по оси t вправо, при 0≤t≤T сигналы перекрываются на интервале от t до Т. Скалярное произведение:

B s (t) =A 2 dt = A 2 (T-t).

При сдвиге копии импульса влево, при -T≤t<0 сигналы перекрываются на интервале от 0 до Т-t. Скалярное произведение:

B s (t) = A 2 dt = A 2 (T+t).

При |t| > T сигнал и его копия не имеют точек пересечения и скалярное произведение сигналов равно нулю (сигнал и его сдвинутая копия становятся ортогональными).

Обобщая вычисления, можем записать:

B s (t) = .

В случае периодических сигналов АКФ вычисляется по одному периоду Т, с усреднением скалярного произведения и его сдвинутой копии в пределах периода:

B s (t) = (1/Т)s(t) s(t-t) dt.

При t=0 значение АКФ в этом случае равно не энергии, а средней мощности сигналов в пределах интервала Т. АКФ периодических сигналов также является периодической функцией с тем же периодом Т. Для однотонального гармонического сигнала это очевидно. Первое максимальное значение АКФ будет соответствовать t=0. При сдвиге копии сигнала на четверть периода относительно оригинала подынтегральные функции становятся ортогональными друг другу (cos w o (t-t) = cos (w o t-p/2) º sin w o t) и дают нулевое значение АКФ. При сдвиге на t=T/2 копия сигнала по направлению становится противоположной самому сигналу и скалярное произведение достигает минимального значения. При дальнейшем увеличении сдвига начинается обратный процесс увеличения значений скалярного произведения с пересечением нуля при t=3T/2 и повторением максимального значения при t=T=2p/w o (cos w o t-2p копии º cos w o t сигнала). Аналогичный процесс имеет место и для периодических сигналов произвольной формы (рис. 2.11).

Отметим, что полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств АКФ.

Для сигналов, заданных на определенном интервале , вычисление АКФ производится с нормировкой на длину интервала :

B s (t) =s(t) s(t+t) dt. (2.26)

Автокорреляция сигнала может оцениваться и функцией автокорреляционных коэффициентов, вычисление которых производится по формуле (по центрированным сигналам):

r s (t) = cos j(t) = ás(t), s(t+t)ñ /||s(t)|| 2 .

Взаимная корреляционная функция (ВКФ) сигналов (cross-correlation function, CCF) показывает как степень сходства формы двух сигналов, так и их взаимное расположение друг относительно друга по координате (независимой переменной), для чего используется та же формула (2.25), что и для АКФ, но под интегралом стоит произведение двух разных сигналов, один из которых сдвинут на время t:

B 12 (t) = s 1 (t) s 2 (t+t) dt. (2.27)

При замене переменной t = t-t в формуле (2.4.3), получаем:

B 12 (t) =s 1 (t-t) s 2 (t) dt =s 2 (t) s 1 (t-t) dt = B 21 (-t)

Рис. 2.12. Сигналы и ВКФ

Отсюда следует, что для ВКФ не выполняется условие четности, а значения ВКФ не обязаны иметь максимум при t = 0. Это можно наглядно видеть на рис. 2.12, где заданы два одинаковых сигнала с центрами на точках 0.5 и 1.5. Вычисление по формуле (2.27) с постепенным увеличением значений t означает последовательные сдвиги сигнала s2(t) влево по оси времени (для каждого значения s1(t) для подынтегрального умножения берутся значения s2(t+t)).

При t=0 сигналы ортогональны и значение B 12 (t)=0. Максимум В 12 (t) будет наблюдаться при сдвиге сигнала s2(t) влево на значение t=1, при котором происходит полное совмещение сигналов s1(t) и s2(t+t). При вычислении значений B 21 (-t) аналогичный процесс выполняется последовательным сдвигом сигнала s1(t) вправо по временной оси с постепенным увеличением отрицательных значений t, а соответственно значения B 21 (-t) являются зеркальным (относительно оси t=0) отображением значений B 12 (t), и наоборот. На рис. 2.13 это можно видеть наглядно.

Рис. 2.13. Сигналы и ВКФ

Таким образом, для вычисления полной формы ВКФ числовая ось t должна включать отрицательные значения, а изменение знака t в формуле (2.27) равносильно перестановке сигналов.

Для периодических сигналов понятие ВКФ обычно не применяется, за исключением сигналов с одинаковым периодом, например, сигналов входа и выхода систем при изучении характеристик систем.

Функция коэффициентов взаимной корреляции двух сигналов вычисляется по формуле (по центрированным сигналам):

r sv (t) = cos j(t) = ás(t), v(t+t)ñ /||s(t)|| ||v(t)||. (2.28)

Значение коэффициентов взаимной корреляции может изменяться от -1 до 1.

2.6. Корреляционно-спектральный анализ детерминированных сигналов. Радиотехнические цепи и сигналы. Часть I

2.6. Корреляционно-спектральный анализ детерминированных сигналов

Во многих радиотехнических задачах часто возникает необходимость сравнения сигнала и его копии, сдвинутой на некоторое время . В частности такая ситуация имеет место в радиолокации, где отраженный от цели импульс поступает на вход приемника с задержкой во времени. Сравнение этих сигналов между собой, т.е. установление их взаимосвязи, при обработке позволяет определять параметры движения цели.

Для количественной оценки взаимосвязи сигнала и его сдвинутой во времени копии вводится характеристика

, (2.57)

Которая называется автокорреляционной функцией (АКФ).

Для пояснения физического смысла АКФ приведем пример, где в качестве сигнала выступает прямоугольный импульс длительностью и амплитудой . На рис. 2.9 изображены импульс, его копия, сдвинутая на интервал времени и произведение . Очевидно, интегрирование произведения дает значение площади импульса, являющегося произведением . Это значение при фиксированном можно изобразить точкой в координатах . При изменении мы получим график автокорреляционной функции.

Найдем аналитическое выражение . Так как

то подставляя это выражение в (2.57), получим

. (2.58)

Если осуществлять сдвижку сигнала влево, то аналогичными вычислениями нетрудно показать, что

. (2.59)

Тогда объединяя (2.58) и (2.59), получим

. (2.60)

Из рассмотренного примера можно сделать следующие важные выводы, распространяющиеся на сигналы произвольной формы:

1. Автокорреляционная функция непериодического сигнала с ростом убывает (необязательно монотонно для других видов сигналов). Очевидно, при АКФ также стремиться к нулю.

2. Своего максимального значения АКФ достигает при . При этом, равна энергии сигнала. Таким образом, АКФ является энергетической характеристикой сигнала. Как и следовало ожидать при сигнал и его копия полностью коррелированны (взаимосвязаны).

3. Из сравнения (2.58) и (2.59) следует, что АКФ является четной функцией аргумента , т.е.

Важной характеристикой сигнала является интервал корреляции . Под интервалом корреляции понимают интервал времени , при сдвижке на который сигнал и его копия становятся некоррелированными.

Математически интервал корреляции определяется следующим выражением

или поскольку – четная функция

. (2.61)

На рис. 2.10 изображена АКФ сигнала произвольной формы. Если построить прямоугольник, по площади равный площади под кривой при положительных значениях (правая ветвь кривой), одна сторона которого равна , то вторая сторона будет соответствовать .

Найдем интервал корреляции для прямоугольного импульса. Подставляя (2.58) в (2.60) после несложных преобразований, получим:

что и следует из рис. 2.9.

По аналогии с автокорреляционной функцией степень взаимосвязи двух сигналов и оценивается взаимной корреляционной функцией (ВКФ)

. (2.62)

Найдем взаимную корреляционную функцию двух сигналов: прямоугольного импульса с амплитудой и длительностью

и треугольного импульса той же амплитуды и длительности

Воспользовавшись (2.61) и вычисляя интегралы отдельно для и , получим:

Графические построения, иллюстрирующие вычисления ВКФ, приведены на рис. 2.11

Здесь пунктирными линиями показано исходное (при ) положение треугольного импульса.

При выражение (2.61) преобразуется в (2.57). Отсюда следует, что АКФ является частным случаем ВКФ при полностью совпадающих сигналах.

Отметим основные свойства ВКФ.

1. Так же, как и автокорреляционная функция, ВКФ является убывающей функцией аргумента . При ВКФ стремиться к нулю.

2. Значения взаимной корреляционной функции при произвольных представляют собой значения взаимной энергии (энергии взаимодействия) сигналов и .

3. При взаимная корреляционная функция (в отличие от автокорреляционной) не всегда достигает максимума.

4. Если сигналы и описываются четными функциями времени, то ВКФ тоже четна. Если же хотя бы один из сигналов описывается нечетной функцией, то ВКФ так же нечетна. Первое утверждение легко доказать, если вычислить ВКФ двух прямоугольных импульсов противоположной полярности

Взаимная корреляционная функция таких сигналов

, (2.63)

является четной функцией аргумента .

Что же касается второго утверждения рассмотренный пример вычисления ВКФ прямоугольного и треугольного импульсов доказывает его.

В некоторых прикладных задачах радиотехники используют нормированную АКФ

, (2.64)

и нормированную ВКФ

, (2.65)

где и – собственные энергии сигналов и . При значение нормированной ВКФ называют коэффициентом взаимной корреляции . Если , то коэффициент взаимной корреляции

Очевидно, значения лежат в пределах от -1 до +1. Если сравнить (2.65) с (1.32), то можно убедиться, что коэффициент взаимной корреляции соответствует значению косинуса угла между векторами и при геометрическом представлении сигналов.

Рассчитаем коэффициент взаимной корреляции для рассмотренных выше примеров. Так как энергия сигнала прямоугольного импульса составляет

а треугольного импульса

то коэффициент взаимной корреляции в соответствии с (2.62) и (2.65) будет равен . Что же касается второго примера, то для двух прямоугольных импульсов одинаковой амплитуды и длительности, но противоположной полярности, .

Экспериментально АКФ и ВКФ могут быть получены с помощью устройства, структурная схема которого изображена на рис. 2.12