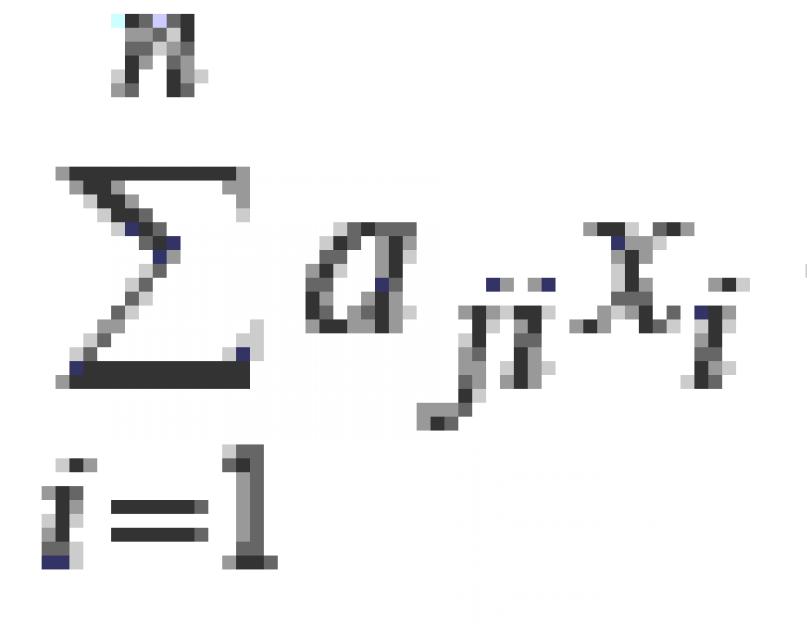Если в условии задачи есть ограничения со знаком ≥, то их можно привести к виду ∑a ji b j , умножив обе части неравенства на -1. Введем m дополнительных переменных x n+j ≥0(j =1,m ) и преобразуем ограничения к виду равенств

(2)

Предположим, что все исходные переменные задачи x 1 , x 2 ,..., x n – небазисные. Тогда дополнительные переменные будут базисными, и частное решение системы ограничений имеет вид

x 1 = x 2 = ... = x n = 0, x n+ j = b j , j =1,m . (3)

Так как при этом значение функции цели F 0 = 0 , можно представить F(x) следующим образом:

F(x)=∑c i x i +F 0 =0 (4)

Начальная симплекс-таблица (симплекс-табл. 1) составляется на основании уравнений (2) и (4). Если перед дополнительными переменными x n+j стоит знак «+», как в (2), то все коэффициенты перед переменными x i и свободный член b j заносятся в симплекс-таблицу без изменения. Коэффициенты функции цели при ее максимизации заносятся в нижнюю строку симплекс-таблицы с противоположными знаками. Свободные члены в симплекс-таблице определяют решение задачи.

Алгоритм решения задачи следующий:

1-й шаг. Просматриваются элементы столбца свободных членов. Если все они положительные, то допустимое базисное решение найдено и следует перейти к шагу 5 алгоритма, соответствующему нахождению оптимального решения. Если в начальной симплекс-таблице есть отрицательные свободные члены, то решение не является допустимым и следует перейти к шагу 2.

2-й шаг. Для нахождения допустимого решения осуществляется , при этом нужно решать, какую из небазисных переменных включить в базис и какую переменную вывести из базиса.

Таблица 1.

x n

базисные переменные	Свободные члены в ограничениях	Небазисные переменные
		x 1	x 2	...	x l	...
x n+1	b 1	a 11	a 12	...	a 1l	...	a 1n
x n+2	b 2	a 21	a 22	...	a 2l	...	a 2n
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n+r	b2	a r1	a r2	...	a rl	...	a rn
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
x n+m	b m	a m1	a m2	...	a ml	...	a mn
F(x) max	F 0	-c 1	-c 2	...	-c 1	...	-c n

Для этого выбирают любой из отрицательных элементов столбца свободных членов (пусть это будет b 2 ведущим, или разрешающим. Если в строке с отрицательным свободным членом нет отрицательных элементов, то система ограничений несовместна и задача не имеет решения.

Одновременно из БП исключается та переменная, которая первой изменит знак при увеличении выбранной НП x l . Это будет x n+r , индекс r которой определяется из условия

т.е. та переменная, которой соответствует наименьшее отношение свободного члена к элементу выбранного ведущего столбца. Это отношение называется симплексным отношением. Следует рассматривать только положительные симплексные отношения.

Строка, соответствующая переменной x n+r , называется ведущей, или разрешающей. Элемент симплекс-таблицы a rl , стоящий на пересечении ведущей строки и ведущего столбца, называется ведущим, или разрешающим элементом. Нахождением ведущего элемента заканчивается работа с каждой очередной симплекс-таблицей.

3-й шаг. Рассчитывается новая симплекс-таблица, элементы которой пересчитываются из элементов симплекс-таблицы предыдущего шага и помечаются штрихом, т.е. b" j , a" ji , c" i , F" 0 . Пересчет элементов производится по следующим формулам:

Сначала в новой симплекс-таблице заполнятся строка и столбец, которые в предыдущей симплекс-таблице были ведущими. Выражение (5) означает, что элемент a" rl на месте ведущего равен обратной величине элемента предыдущей симплекс-таблицы. Элементы строки a ri делятся на ведущий элемент, а элементы столбца a jl также делятся на ведущий элемент, но берутся с противоположным знаком. Элементы b" r и c" l рассчитываются по тому же принципу.

Остальные формулы легко записать с помощью .

Прямоугольник строится по старой симплекс-таблице таким образом, что одну из его диагоналей образует пересчитываемый (a ji) и ведущий (a rl) элементы (рис. 1). Вторая диагональ определяется однозначно. Для нахождения нового элемента a" ji из элемента a ji вычитается (на это указывает знак « – » у клетки) произведение элементов противоположной диагонали, деленное на ведущий элемент. Аналогично пересчитываются элементы b" j , (j≠r) и c" i , (i≠l).

4-й шаг. Анализ новой симплекс-таблицы начинается с 1-го шага алгоритма. Действие продолжается, пока не будет найдено допустимое базисное решение, т.е. все элементы столбца свободных членов должны быть положительными.

5-й шаг. Считаем, что допустимое базисное решение найдено. Просматриваем коэффициенты строки функции цели F(x) . Признаком оптимальности симплекс-таблицы является неотрицательность коэффициентов при небазисных переменных в F-строке.

Рис. 1. Правило прямоугольника

Если среди коэффициентов F-строки имеются отрицательные (за исключением свободного члена), то нужно переходить к другому базисному решению. При максимизации функции цели в базис включается та из небазисных переменных (например x l), столбцу которой соответствует максимальное абсолютное значение отрицательного коэффициента c l в нижней строке симплекс-таблицы. Это позволяет выбрать ту переменную, увеличение которой приводит к улучшению функции цели. Столбец, соответствующий переменной x l , называется ведущим. Одновременно из базиса исключается та переменная x n+r , индекс r которой определяется минимальным симплексным отношением:

Строка, соответствующая x n+r , называется ведущей , а элемент симплекс-таблицы a rl , стоящий на пересечении ведущей строки и ведущего столбца, называется ведущим элементом.

6-й шаг. по правилам, изложенным на 3-м шаге. Процедура продолжается до тех пор, пока не будет найдено оптимальное решение или сделан вывод, что оно не существует.

Если в процессе оптимизации решения в ведущем столбце все элементы неположительные, то ведущую строку выбрать невозможно. В этом случае функция в области допустимых решений задачи не ограничена сверху и F max ->&∞.

Если же на очередном шаге поиска экстремума одна из базисных переменных становится равной нулю, то соответствующее базисное решение называется вырожденным. При этом возникает так называемое зацикливание, характеризующееся тем, что с определенной частотой начинает повторяться одинаковая комбинация БП (значение функции F при этом сохраняется) и невозможно перейти к новому допустимому базисному решению. Зацикливание является одним из основных недостатков симплекс-метода, но встречается сравнительно редко. На практике в таких случаях обычно отказываются от ввода в базис той переменной, столбцу которой соответствует максимальное абсолютное значение отрицательного коэффициента в функции цели, и производят случайный выбор нового базисного решения.

Пример 1. Решить задачу

max{F(x) = -2x 1 + 5x 2 | 2x 1 + x 2 ≤7; x 1 + 4x 2 ≥8; x 2 ≤4; x 1,2 ≥0}

Симплексным методом и дать геометрическую интерпретацию процесса решения.

Графическая интерпретация решения задачи представлена на рис. 2. Максимальное значение функции цели достигается в вершине ОДЗП с координатами . Решим задачу с помощью симплекс-таблиц. Умножим второе ограничение на (-1) и введём дополнительные переменные, чтобы неравенства привести к виду равенств, тогда

Исходные переменные x 1 и x 2 принимаем в качестве небазисных, а дополнительные x 3 , x 4 и x 5 считаем базисными и составляем симплекс-таблицу(симплекс-табл. 2). Решение, соответствующее симплекс-табл. 2, не является допустимым; ведущий элемент обведен контуром и выбран в соответствии с шагом 2 приведенного ранее алгоритма. Следующая симплекс-табл. 3 определяет допустимое базисное решение, ему соответствует вершина ОДЗП на рис. 2 Ведущий элемент обведен контуром и выбран в соответствии с 5-м шагом алгоритма решения задачи. Табл. 4 соответствует оптимальному решению задачи, следовательно: x 1 = x 5 = 0; x 2 = 4; x 3 = 3; x 4 = 8; F max = 20.

Рис. 2. Графическое решение задачи

Один из методов решения оптимизационных задач (как правило связанных с нахождением минимума или максимума ) линейного программирования называется . Симплекс-метод включает в себя целую группу алгоритмов и способов решения задач линейного программирования. Один из таких способов, предусматривающий запись исходных данных и их пересчет в специальной таблице, носит наименование табличного симплекс-метода .

Рассмотрим алгоритм табличного симплекс-метода на примере решения производственной задачи , которая сводится к нахождению производственного плана обеспечивающего максимальную прибыль.

Исходные данные задачи на симплекс-метод

Предприятие выпускает 4 вида изделий, обрабатывая их на 3-х станках.

Нормы времени (мин./шт.) на обработку изделий на станках, заданы матрицей A:

Фонд времени работы станков (мин.) задан в матрице B:

Прибыль от продажи каждой единицы изделия (руб./шт.) задана матрицей C:

Цель производственной задачи

Составить такой план производства, при котором прибыль предприятия будет максимальной.

Решение задачи табличным симплекс-методом

(1) Обозначим X1, X2, X3, X4 планируемое количество изделий каждого вида. Тогда искомый план: (X1, X2, X3, X4 )

(2) Запишем ограничения плана в виде системы уравнений:

(3) Тогда целевая прибыль:

То есть прибыль от выполнения производственного плана должна быть максимальной.

(4) Для решения получившейся задачи на условный экстремум, заменим систему неравенств системой линейных уравнений путем ввода в нее дополнительных неотрицательных переменных (X5, X6, X7 ).

(5) Примем следующий опорный план :

X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80

(6) Занесем данные в симплекс-таблицу :

В последнюю строку заносим коэффициенты при целевой функции и само ее значение с обратным знаком;

(7) Выбираем в последней строке наибольшее (по модулю ) отрицательное число.

Вычислим b = Н / Элементы_выбранного_столбца

Среди вычисленных значений b выбираем наименьшее .

Пересечение выбранных столбца и строки даст нам разрешающий элемент. Меняем базис на переменную соответствующую разрешающему элементу (X5 на X1 ).

• Сам разрешающий элемент обращается в 1.
• Для элементов разрешающей строки – a ij (*) = a ij / РЭ (то есть каждый элемент делим на значение разрешающего элемента и получаем новые данные ).
• Для элементов разрешающего столбца – они просто обнуляются.
• Остальные элементы таблицы пересчитываем по правилу прямоугольника.

a ij (*) = a ij – (A * B / РЭ)

Как видите, мы берем текущую пересчитываемую ячейку и ячейку с разрешающим элементом. Они образуют противоположные углы прямоугольника. Далее перемножаем значения из ячеек 2-х других углов этого прямоугольника. Это произведение (A * B ) делим на разрешающий элемент (РЭ ). И вычитаем из текущей пересчитываемой ячейки (a ij ) то, что получилось. Получаем новое значение - a ij (*) .

(9) Вновь проверяем последнюю строку (c ) на наличие отрицательных чисел . Если их нет – оптимальный план найден, переходим к последнему этапу решения задачи. Если есть – план еще не оптимален, и симплекс-таблицу вновь нужно пересчитать.

Так как у нас в последней строке снова имеются отрицательные числа, начинаем новую итерацию вычислений.

(10) Так как в последней строке нет отрицательных элементов, это означает, что нами найден оптимальный план производства! А именно: выпускать мы будем те изделия, которые перешли в колонку «Базис» - X1 и X2. Прибыль от производства каждой единицы продукции нам известна (матрица C ). Осталось перемножить найденные объемы выпуска изделий 1 и 2 с прибылью на 1 шт., получим итоговую (максимальную! ) прибыль при данном плане производства.

ОТВЕТ:

X1 = 32 шт., X2 = 20 шт., X3 = 0 шт., X4 = 0 шт.

P = 48 * 32 + 33 * 20 = 2 196 руб.

Галяутдинов Р.Р.

© Копирование материала допустимо только при указании прямой гиперссылки на

Читайте также: V2: ДЕ 57 - Фундаментальная система решений линейного однородного дифференциального уравнения Б1 2. Линейный оператор в конечномероном пространстве, его матрица. Характеристический многочлен линейного оператора. Собственные числа и собств векторы. Базовые управляющие структуры структурного программирования Билет 13 Угол между 2 мя прямыми, условия параллельности и перпендикулярности. Преобразование линейного оператора при переходе к новому базису Билет 13. Линейные операторы. Матрица линейного оператора. Билет 26. Корневые подпространства. Расщепление линейного пространства в прямую сумму корневых подпространств. Билет 27. Жорданов базис и жорданова матрица линейного оператора в комплексном пространстве. Билет 35. Эрмитовы операторы и эрмитовы матрицы. Эрмитого разложение линейного оператора. Билет 7 Скалярное произведение векторов, проекция одного вектора на другой. Понятие линейного пространства и подпространства, критерии подпространства

Теорема (о выборе разрешающего элемента)

Если в нескольких столбцах z-ой строке есть отрицательные элементы, то разрешающим столбцом нужно выбрать тот столбец у которого максимально произведение абсолютного значения коэффициента в z-ой строке и минимально симплексное отношение данном столбце.

Доказательство:

Пусть разрешающим будет элемент . В результате шага модифицированных жордановых исключений свободным членом в z-строке будет число , равное .Поскольку и ,скобка в этом выражении всегда будет положительной. А так как значение функционала всегда равно свободному члену, эта скобка представляет собой тот добавок к функционалу, который получается в результате сделанного шага.

Чем большее приращение будет получать функционал на каждом шаге, тем меньше потребуется шагов (т.е. вычислений) для достижения оптиума. Величина этого приращения зависит от абсолютной величины коэффициента и от величины наименьшего симплексного отношения . То есть разрешающим столбцом будет столбец, у которого максимально это произведение.

Пример: линейное программирование:

Найдем максимум функции

при ограничениях

Решение: составим жорданову таблицу.

Поскольку в ней свободные члены положительны, план является опорным. Однако он не оптимален, так как коэффициенты z-строки отрицательны. Выбираем из них тот, у которого наибольшее произведение абсолютной величины и наименьшее симплексное отношение. Третий столбец считаем разрешающим, так как он имеет наибольшую абсолютную величину 8 и симплексные отношения: соответственно ( , поэтому элемент 1 в третьим столбце будет разрешающим). Делаем шаг модифицированных жордановых исключений и приходим к следующей таблице.

Судя по коэффициентам z-строки, в полученной таблице оптимальное решение не достигнуто. Берём второй столбец с отрицательным коэффициентом в z-строке за разрешающий (разрешающей строкой может быть только первая). С найденным элементом 5 делаем следующий шаг.

В z-строке все коэффициенты положительны, план, получаемый приравниванием верхних переменных нулю, а боковых – свободным членам, оптимален. Выписываем из таблицы значения основных неизвестных: Максимальное значение функционала считаем в последней клетке таблицы:

В окончательной таблице все определители неотрицательны. Это говорит о том, что при значениях неизвестных функционал достигает максимума

Обычно предполагается, что на множестве планов задачи нет точек, в которых знаменатель целевой функции равен нулю. Без ограничения общности, можно считать, что .

В задаче дробно-линейного программирования экстремум целевой функции достигается в вершине многогранника решений. Это сходство с линейным программированием позволяет решать дробно-линейные задачи методом Штифеля.

Вычисления оформляются в виде жордановых таблиц. При этом для функционала отводятся две нижние строки: в первую из них записываем коэффициенты числителя, а во вторую – знаменателя. Исходной задаче соответствует таблица 1:

	–x 1	–x 2	…	–x j	…	–x n
y 1	a 11	a 12	…	a 1 j	…	a 1 n	a 1
…	………………………………………	…
y i	a i 1	a i 2	…	a ij	…	a in	a i
…	………………………………………	…
y m	a m 1	a m 2	…	a mj	…	a mn	a m
z 1	–p 1	–p 2	…	–p j	…	–p n
z 2	–q 1	–q 2	…	–q j	…	–q n

Через y i обозначаются разности между правыми и левыми частями системы ограничений:

y i = a i – a i 1 x 1 – a i 2 x 2 – a i 3 x 3 – … – a in x n ³ 0.

Свободными переменными мы будем называть переменные, расположенные в верхней заглавной строке жордановой таблицы. Придавая свободным переменным нулевые значения, мы получим исходное базисное решение: . Данный вектор не может являться опорным планом, т.к. знаменатель целевого функционала на нем равен нулю (z 2 = 0). Поэтому среди свободных членов системы ограничений a 1 ,…, a m обязательно есть отрицательные числа (иначе базисное решение было бы опорным планом).

Шагами модифицированных жордановых исключений, точно так же, как при решении задачи линейного программирования (см. ), отыскиваем первоначальный план задачи. В результате k шагов мы приходим к таблице 2:

	–y 1	…	–x j	…	–x n
x 1	b 11	…	b 1 j	…	b 1 n	b 1
.…	………………………………………
y i	b i 1	…	b ij	…	b in	b i
….	…………………………………….
y m	b m 1	…	b mj	…	b mn	b m
z 1	f 1	…	f j	…	f n	F
z 2	g 1	…	g j	…	g n	G

В таблице 2 все свободные члены b i неотрицательны, что обеспечивает неотрицательность базисных переменных x 1 ,…, y m . Кроме того (в силу положительности знаменателя целевой функции z 2 на множестве опорных планов). Первоначальным опорным планом является вектор с координатами . Значение целевой функции на первоначальном опорном плане равно .

Заметим, что если на одном из шагов жордановых исключений какой-либо из свободных членов b i окажется отрицательным, а все остальные элементы i -й строки будут неотрицательными, то задача не будет иметь решения из-за отсутствия планов.

Проследим за тем, как меняется целевая функция при переходе от одного опорного плана задачи к другому. Оказывается, знак разности между новым и старым значениями функции совпадает со знаком определителя . Если. Т.к. многогранник решений содержит лишь конечное число опорных планов, то за конечное число шагов мы придем к оптимальному опорному плану.

Этому процессу может помешать только неограниченность многогранника решений. В этом случае целевая функция может иметь так называемый асимптотический экстремум (в данном случае – максимум). Асимптотическим максимумом задачи дробно-линейного программирования называется точная верхняя грань целевой функции на множестве планов, которая не достигается ни на одном из планов. В том случае, когда задача имеет асимптотический максимум, в области планов всегда можно найти такой план (не опорный), на котором целевая функция принимает значение сколь угодно близкое к асимптотическому максимуму.

Метод Штифеля позволяет находить не только максимум, но и асимптотический максимум задачи дробно-линейного программирования. Рассмотрим более подробно переход от плана к плану и выясним. Выбирая разрешающий элемент в j -м столбце, мы должны руководствоваться принципом минимального симплексного отношения. Т.е. разрешающий элемент в j -м столбце должен попасть в ту строку, для которой симплексное отношение положительно и минимально.

Т.к. после нахождения первоначального опорного плана все правые части b i стали неотрицательными, то разрешающим элементом j -го столбца может быть один из его положительных элементов (). Если на каждом шаге этапа поиска оптимального опорного плана в выбранном разрешающем столбце присутствует (хотя бы один) положительный элемент , то такая задача имеет максимум (возможно, что не один).

Однако, если на одном из шагов некоторая оценка меньше нуля, и при этом все элементы j -го столбца . Тогда в данном столбце, руководствуясь принципом минимального симплексного отношения, разрешающий элемент выбирать нельзя. Увеличивая значения свободной переменной x j от 0 и до (см. Табл. 2), мы все время остаемся в области планов. Это связано с тем, что увеличение переменной x j не вызывает изменения знака на минус ни у одной из базисных переменных.

Обозначим через М предел, к которому, монотонно возрастая, стремится целевая функция при : . Это число является асимптотическим максимумом.

| 2 |

Приведенные выше преобразования удобно выполнять в специальных таблицах, называемых симплекс-таблицами.

В симплекс-таблице выделяются следующие блоки:

Запишем решение задачи примера из раздела 3.3 в симплекс-таблицах:

Все исходные данные, содержащиеся в математическом условии задачи, переносятся в первую симплексную таблицу. Зануляя свободные переменные, получаем опорный план

В последнюю строку первой симплекс-таблицы заносим критерий в неявной форме

Исключаем из этого критерия базисную переменную x 4 , приводя критерий к виду

Для оптимальности решения все оценки должны быть неотрицательны

Решение не оптимальное, т.к. есть отрицательные оценки.

Оценки могут быть вычислены по формулам. Произведение представляет из себя, текущий вектор матрицы условий, тогда оценку свободной переменной можно вычислить как скалярное произведение вектора коэффициентов при базисных переменных на текущий вектор матрицы условий минус коэффициент целевой функции при этой переменной. Так, для получаем значение

Разрешающим столбцом выбираем тот, где наименьшая по величине оценка (если задача на максимум). А для выбора разрешающей строки нужно среди всех строк найти, выраженная из которой переменная, уменьшаясь, которая быстрее обращается в ноль.

В итоге, мы получаем, что разрешающий столбец - , а разрешающая строка - . Значит из списка базисных выходит переменная и входит переменная.

Решение не оптимальное, т.к. есть отрицательная оценка -2.

Решение оптимальное, т.к. все оценки больше нуля. Очевидно, что увеличить нельзя.

Правила построения симплекс-таблиц

Симплекс-таблица строится для какого-либо опорного решения.

Пусть опорное решение. Симплекс-таблица для этого решения имеет вид

Базисная матрица B = (A 1 , A 2 , … A m)

· при базисных переменных текущая матрица единичная.

• · любой столбец.
• · вектор правых частей ограничений.
• · оценки при свободных переменных не нулевые

· в правой нижней клетке - значение критерия

Этапы симплекс-метода

• 1. Проверка признака оптимальности ()
• 2. Если есть, то решение не оптимальное. Тогда выбираем столбец с минимальной оценкой. Его назовем разрешающим.
• 3. Разрешающая строка выбирается по минимальному отношению свободных членов к положительным коэффициентам разрешающего столбца. Базисная переменная, выражающаяся из этой строки, выходит из списка базисных переменных. Т.е. x k выходит, а x s входит.

• 4. Текущая симплекс-таблица преобразуется по следующему правилу:
  • · разрешающая строка делится на разрешающий элемент:

• · разрешающий столбец заменяется единичным.
• · все остальные элементы симплекс-таблицы могут быть пересчитаны по правилу четырехугольника:

Мысленно строится четырехугольник на диагонали, соединяющей искомый элемент с разрешающим. Тогда новое значение элемента равно прежнему значению минус произведение элементов на противоположной диагонали, деленное на разрешающий элемент.

Или новое значение элемента равно произведению элементов на главной диагонали минус произведение элементов на противоположной диагонали, и все это деленное на разрешающий элемент.

Замечание : Если в разрешающей строке был нулевой элемент, значит этот столбец не меняется; если в разрешающем столбце есть нулевой элемент, то соответствующая строка не меняется.

Как известно, метод Жордана-Гаусса, он же метод последовательного исключения неизвестных, является модификацией метода Гаусса решения систем линейных алгебраических уравнений (СЛАУ).

Метод базируется на элементарных преобразованиях (переводящих систему в эквивалентную), к которым относятся:

• прибавление к обеим частям уравнения системы другого уравнения той же системы, умноженного на число, отличное от нуля;
• перестановка местами уравнений в системе;
• удаление из системы уравнений вида 0 = 0.

В отличие от метода Гаусса, на каждом шаге одна переменная исключается из всех уравнений, кроме одного.

Шаг метода состоит в следующем:

• выбрать в очередном уравнении неизвестное с коэффициентом, отличным от нуля (разрешающим элементом);
• разделить выбранное уравнение на разрешающий элемент;
• с помощью выбранного уравнения исключить неизвестное при разрешающем элементе из всех остальных уравнений;
• на следующем шаге аналогично исключается другое неизвестное из всех уравнений, кроме одного;
• процесс продолжается, пока не будут использованы все уравнения.

Алгоритмизировать это можно так:

Для СЛАУ в матричном виде A*x=b (матрица A размерности m*n , совсем необязательно квадратная) составляется следующая таблица:

В таблице выбран разрешающий элемент a r,s ≠0 , тогда r - разрешающая строка, s - разрешающий столбец.

Переход к следующей таблице выполняется по правилам:

1. вычисляются элементы разрешающей строки: a" r,j =a r,j /a r,s - то есть, r-строка таблицы делится на разрешающий элемент;

2. все элементы разрешающего столбца, кроме a r,s , равного единице, становятся равны нулю;

3. элементы вне разрешающих строки и столбца вычисляются по формуле, изображённой ниже:

Легко не запутаться, если увидеть, что числитель этой формулы похож на вычисление определителя матрицы 2 на 2.

4. При ручном расчёте значение в последнем контрольном столбце сравнивается с суммой предыдущих элементов строки. Если значения не совпадают, ошибки надо искать в данной строке. При автоматизированном расчёте контрольный столбец можно опустить.

Возможны следующие случаи:

1. В процессе исключений левая часть уравнения системы обращается в 0, а правая b≠0 , тогда система не имеет решения.

2. Получается тождество 0 = 0 - уравнение является линейной комбинацией остальных и строка нулей может быть вычеркнута из системы.

3. После использования всех уравнений для исключения неизвестных, таблица либо содержит искомое решение, либо показывает несовместность системы ограничений.

Запрограммируем метод в Excel одной формулой, изменять которую должно быть не слишком трудоёмко. Например, для решения СЛАУ

заполним коэффициентами системы ячейки листа от A1 до D4 включительно, выберем разрешающий элемент a 1,1 =1 , а первый шаг метода сделаем в ячейке A6 , куда загоним "универсальную" формулу для преобразования Жордана-Гаусса:

ЕСЛИ(СТРОКА($A$1)=СТРОКА(A1);A1/$A$1;
ЕСЛИ(СТОЛБЕЦ($A$1)=СТОЛБЕЦ(A1);0;(A1*$A$1-
ДВССЫЛ(АДРЕС(СТРОКА(A1);СТОЛБЕЦ($A$1)))*
ДВССЫЛ(АДРЕС(СТРОКА($A$1);СТОЛБЕЦ(A1))))/$A$1))

На следующем шаге разрешающим элементом может быть, например, a 2,2 =1 (ячейка B7). Нам останется скопировать формулу из A6 в A11 (по пустой строке оставляем, чтоб визуально разделить шаги метода), войти в режим редактирования формулы (двойной щелчок по ячейке или выбрать её и нажать клавишу F2) и поправить (аккуратно перетащить мышкой за границу) все закреплённые ссылки с ячейки A1 на B7 .

Конечно, можно заменить везде в формуле закреплённую ссылку $A$1 на конструкцию вида ДВССЫЛ(ЯЧЕЙКА) , образующую динамический адрес ссылки. Скажем, ДВССЫЛ(F8) , а в ячейке F8 будет автоматически формироваться адрес ячейки разрешающего элемента по заданным пользователем номеру строки и столбца. Тогда для этих номеров строки и столбца придётся предусмотреть отдельные ячейки, например, так:

Увы, всё это ничего не даст - вместо $A$1 мы просто вынуждены будем закрепить в формуле ДВССЫЛ($F$8) и всё равно потом перетаскивать столько же ссылок при копировании формулы. Кроме того, "вручную" введённые номера строки и столбца придётся ещё и проверять на допустимость (хотя бы как на рисунке), так что, не будем умножать сущностей.

Посмотреть метод в работе можно на двух первых листах приложенного файла Excel (2 разных примера).

На преобразовании Жордана-Гаусса основан и такой универсальный метод решения линейных задач оптимизации, как симплекс-метод . Описания его обычно страшны, длинны и перегружены теоремами. Попробуем сделать простое описание и разработать пригодный для расчёта в Excel алгоритм. На самом деле, симплекс-метод уже встроен в стандартную надстройку Пакет анализа, и программировать его "вручную" не нужно, так что наш код имеет, скорее, учебную ценность.

Сначала минимум теории.

Если вектор-столбцы СЛАУ линейно независимы, соответствующие им переменные являются базисными , а остальные – свободными . Например, в СЛАУ

переменные x 2 и x 4 - базисные, а x 1 и x 3 - свободные. Базисные переменные между собой независимы, а свободные можно сделать, например, нулями и получить { x 2 =2, x 4 =1 } – базисное решение системы.

Выбирая различные разрешающие элементы, можно получить решения СЛАУ с различными базисами. Любое неотрицательное базисное решение СЛАУ называется опорным .

Симплекс-метод обеспечивает переход от одного опорного решения к другому, пока не будет достигнуто оптимальное решение, дающее минимум целевой функции.

Алгоритм симплекс-метода состоит в следующем:

1. Задача ЛП преобразуется к каноническому виду:

Это всегда можно сделать следующим образом: к задаче, записанной в стандартной постановке

добавляются дополнительные балансовые переменные , число которых соответствует числу ограничений-неравенств m (ограничения на неотрицательность значений неизвестных не учитываются). После этого неравенства со знаком " ≤ " превращаются в равенства, например, система ограничений вида

2*x 1 +3*x 2 ≤20
3*x 1 +x 2 ≤15
4*x 1 ≤16
3*x 2 ≤12
x 1 ,x 2 ≥0

примет вид

2*x 1 +3*x 2 +x 3 =20
3*x 1 +x 2 +x 4 =15
4*x 1 +x 5 =16
3*x 2 +x 6 =12
x 1 ,x 2 ,...,x 6 ≥0

То есть, "экономический" смысл балансовых переменных очень прост – это "остатки" неиспользованных ресурсов каждого вида.

Если в исходной задаче искался не минимум, а максимум, целевая функция Z заменятся на Z 1 = -Z . Решения задач совпадают, при этом min Z = - max Z 1 . Например, цель

Z(x 1 ,x 2)=2*x 1 +5*x 2 (max)

переписывается в виде

Z 1 (x 1 ,x 2)=-2*x 1 -5*x 2 (min)

Если в исходной задаче были уравнения-неравенства со знаками " ≥ " вместо " ≤ ", обе части каждого такого неравенства умножаются на -1 , а знак неравенства меняется на противоположный, например,

3*x 1 +x 2 +x 4 ≥15

превращается в

3*x 1 -x 2 -x 4 ≤15

Канонический вид модели получен, для него выписывается симплекс-таблица :

В левом столбце записываются базисные переменные (БП), если они ещё не выделены – пусто.

2. С помощью шагов Жордана–Гаусса ищется первоначальный опорный план, т.е. СЛАУ приводится к базисному виду с неотрицательными свободными членами b i >0 . При этом целевая функция Z должна быть выражена только через свободные неизвестные (нулевые коэффициенты в Z-строке стоят только под переменными x i , которые есть в базисе). При выборе разрешающего элемента a r,s в строку r столбца БП выписываем переменную x s , если там уже была переменная – вычеркиваем её (выводим из базиса).

3. Выписываем под столбцами x i опорный план X * : под свободными переменными - нули, под базисными – соответствующие базисной переменной коэффициенты из столбца b .

Ниже выписываем вектор R по правилу: под базисными переменными – нули, под свободными R i =Z i .

Если все R i ≥0 , найдено оптимальное решение X * и значение цели Z min = -q , иначе нужен новый план, а у вас он есть, товарищ Жюков? (п. 4).

4. Для выбора разрешающего столбца s выбираем максимальную по модулю отрицательную компоненту вектора R , разрешающий столбец s выбран. Затем анализируем коэффициенты s-го столбца матрицы системы ограничений. Если все a i,s ≤0 , решения нет и Z min стремится к минус бесконечности, иначе переходим к п.5.

5. Для выбора разрешающей строки r составляем неотрицательные отношения b i /A i,s ≥0 , i=1,2,...,m , и выбираем среди них наименьшее. Если минимум достигается для нескольких строк, за разрешающую можно принять любую из них, при этом, в новом опорном плане значения некоторых базисных переменных станут равными 0, т.е., получаем вырожденный опорный план.

6. Выполняем преобразование Жордана-Гаусса с разрешающим элементом a r,s и переходим к п.3

Геометрически симплекс-методу соответствует кратчайший обход вершин n-мерного выпуклого многогранника, образующего область допустимых решений задачи:

Здесь мы перешли от опорного плана C , представляющего собой одну из вершин многомерного многоугольника, к оптимальному плану E=X * .

Запрограммировать это всё в Excel нелегко, но можно. В прилагаемом документе приведены 3 примера, реализующие решение задач симплекс-методом. Правда, при выполнени шага менять уже придётся 3 формулы, на листе первого примера на симплекс-метод они выделены жёлтым цветом: расчёт отношений для выбора разрешающей строки в ячейке I2 , заполнение столбца БП в ячейке A12 , шаг преобразования Жордана-Гаусса в ячейке B12 . Как и в примере на преобразование Жордана-Гаусса, изменение формул связано только с необходимостью сослаться на новую строку, содержащую адрес ячейки с разрешающим элементом (для первого шага - ячейка C9).