Линейное программирование представляет собой один из наиболее значимых разделов математики, где осуществляется изучение теоретических и методических основ решения определенных задач. Данная математическая дисциплина широко используется в последние годы в разнообразных экономических и технических областях, где не последняя роль отведена математическому планированию и использованию автоматических систем вычисления. Этот раздел науки посвящен изучению линейных оптимизационных моделей. То есть линейное программирование посвящено числам. Впервые данный термин был предложен Т. Купмансом в 1951 году. Оптимальный план каждой линейной программы необходимо автоматически связывать с оптимальным уровнем цен, то есть с объективно обусловленными оценками.
Линейное программирование: методы
При помощи методики удается решить немалое количество экстремальных задач, что связаны с экономикой. В данном случае обычно требуется найти крайние значения некоторых функций переменной величины. В качестве основы линейного программирования выражено решение системы преобразуемых в уравнения и неравенства. Данный вид программирования характеризуется математической формулировкой переменных величин, последовательностью и определенным порядком расчетов, а также логическим анализом. Это применимо:
Если имеется математическая определенность и количественная ограниченность между изучаемыми факторами и переменными величинами;
Если имеется взаимозаменяемость факторов благодаря последовательности расчетов;
В случае если математическая логика совмещена с пониманием сущности явлений, которые изучаются.
Линейное программирование в способствует исчислению оптимальной производительности всех машин, поточных линий, агрегатов, а также решению задач рационального применения имеющихся материалов.
В сельском хозяйстве при помощи данного метода определяется минимальная стоимость рациона кормежки с учетом имеющегося количества корма. При этом учитываются виды и содержание в них определенных полезных веществ.
В литейном производстве данная методика позволяет найти решение транспортной задачи и задачи о смесях, которые входят в состав металлургической шихты. Суть транспортной задачи в данном случае подразумевает оптимальное прикрепление потребляющих предприятий к предприятиям, которые заняты производством продукции.
Линейное программирование: задачи
Отличительной чертой всех экономических задач, которые решаются посредством методики линейного программирования, является выбор определенных вариантов решения, а также ограничивающих условий. Благодаря решению такой задачи удается найти оптимальное решение из всех альтернативных вариантов.
Значительной ценностью использования методики линейного программирования в экономике служит выбор самого оптимального варианта из большого количества всех вариантов, которые считаются допустимо возможными. Подобные задачи почти нереально решить иными способами, так как только они позволяют найти степень рациональности применения При помощи линейного программирования разрешается такая основная задача, как транспортная, которая должна минимизировать грузооборот продукции широкого потребления в процессе их доставки от производителя.
Линейное программирование в Excel
В процессе решения таких задач для начала необходимо составить модель, что подразумевает формулировку условий на математическом языке. После этого этапа можно найти решение посредством графического метода. Для этого в программе Excel существует специальная функция «Поиск решения».
Как уже понятно из вышесказанного, линейное программирование имеет весьма обширную сферу применения.
Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.
Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1)
;
(1.2)
Здесь ,
есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки ,
так и знаки .
Построение области допустимых решений
Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.
Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой .
С одной стороны от этой прямой ,
а с другой стороны .
На самой прямой .
Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).
Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.
Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.
Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.
Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).
Нахождение экстремума целевой функции
Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.
Теперь мы можем искать экстремум целевой функции
(1.1)
.
Для этого выбираем любое число и строим прямую
(3)
.
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна .
такая прямая называется линией уровня функции .
Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение .
С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение .
Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .
Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.
Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.
Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.
Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и ,
включая сами точки и .
Пример решения задачи линейного программирования графическим методом
Условие задачи
Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида - 10 м, третьего вида - 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В - 300 ден. ед.
Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.
Решение
Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)
Тогда экономико-математическая модель задачи имеет вид:
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).
Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.
(П1.1)
.
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).
Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и .
Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания ,
и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.
Пример 2
Условие задачи
Решить задачу линейного программирования графическим методом.
Решение
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).
Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).
Строим прямую .
Строим прямую (ось абсцисс).

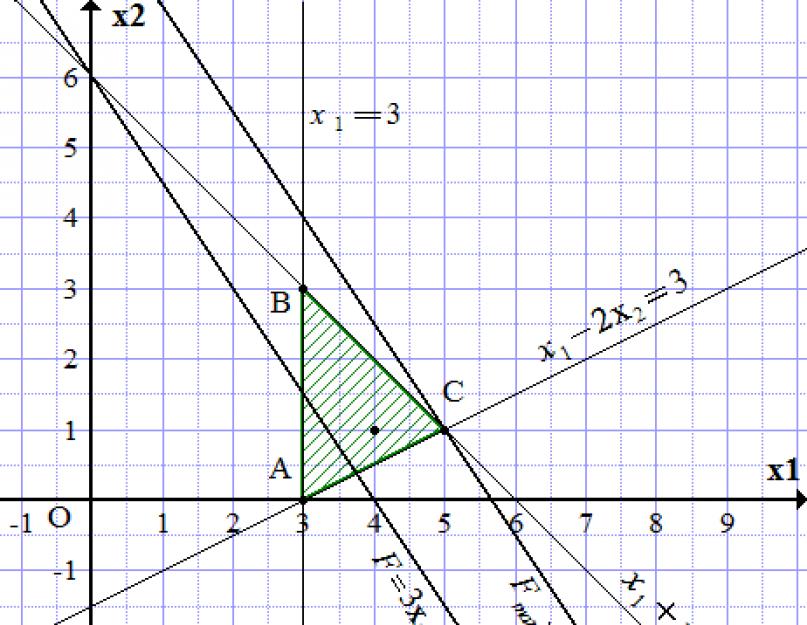
Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.
Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и ,
то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания ,
и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
Пример отсутствия решения
Условие задачи
Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.
Решение
Решаем задачу графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).
Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.
Строим произвольную линию уровня целевой функции, например,
(П3.1)
.
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .
Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.
Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания ,
и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:
Ответ
Максимального значения не существует.
Минимальное значение
.
Большое число экономических задач сводится к линейным математическим моделям. Традиционно их называют моделями линейного программирования. Под линейным программированием понимается линейное планирование, т.е. получение оптимального плана-решения в задачах с линейной структурой. Обычно его используют специалисты штабных подразделений для разрешения производственных трудностей. Типичными примерами применений модели линейного программирования являются следующие:
укрупненное планирование производства (составление графиков производства, минимизирующих общие издержки в связи с изменением ставки процента);
планирование ассортимента изделий (определение оптимальной структуры производства продуктов питания для человека);
маршрутизация производства изделий (определение оптимального технологического маршрута изготовления изделия);
регулирование запасов (определение оптимального сочетания продуктов на складе);
календарное планирование производства (составление календарных планов, минимизирующих издержки с учетом расходов на содержание запасов, оплату сверхурочной работы и заказов на стороне);
планирование распределения продукции и пр.
В самом общем виде линейное программирование сводится к оптимизационной задаче и записывается в следующем виде:
Чтобы
решить задачу оптимизации, достаточно
найти ее оптимальное решение, т.е. указать
 такое,
чтоf
(X
0
)≥
f
(X
)
при любом
такое,
чтоf
(X
0
)≥
f
(X
)
при любом
 ,
или для случая минимизации -f
(X
0
)≤
f
(X
)
при любом
,
или для случая минимизации -f
(X
0
)≤
f
(X
)
при любом
 .
.
Оптимизационная задача является неразрешенной, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешенной, если целевая функция f (X ) не ограничена сверху на допустимом множестве W .
Методы решения оптимизационных задач зависят как от вида целевой функции f (X ) , так и от строения допустимого множества W . Если целевая функция в задаче является функцией п переменных, то методы решения называются методами математического программирования.
Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:
|
| ||
При этом система линейных уравнений (2) и неравенств (3), (4), определяющая допустимое множество решений задачи W , называется системой ограничений задачи линейного программирования, а линейная функция f (X ) называется целевой функцией, или критерием оптимальности.
Если математическая модель задачи линейного программирования имеет вид:
|
| ||
|
| ||
|
| ||
|
|
то говорят, что задача представлена в канонической форме.
Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме, переводя максимизацию к минимизации, от ограничений неравенств к ограничениям равенств и заменяя переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком и наоборот.
Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:
1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;
2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1);
3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных, они преобразуются в равенства;
4) если некоторая переменная x k не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными: x k = x ’ k - x 1 , где 1 – свободный индекс, x ’ k ≥ 0, x 1 ≥ 0.
Обобщая сказанное можно сделать следующие выводы:
1. Ограничения в задачах линейного программирования могут быть выражены как равенствами, так и неравенствами.
2. Линейная функция может стремиться как к максимуму, так и к минимуму.
3. Переменные в модели всегда неотрицательны.
4. От любой задачи линейного программирования можно перейти к канонической (основной) задаче линейного программирования.
Каждой задаче линейного программирования можно противопоставить другую задачу линейного программирования, двойственную по отношению к исходной (прямой).
Рассмотрим задачу линейного программирования следующего вида:
|
……………………….. |
В задаче требуется максимизировать целевую функцию; все ограничения являются неравенствами со знаком ≤, все переменные х 1 , х 2 ,…,х п п управляющих переменных и m ограничений. Коэффициенты при переменных в целевой функции: c 1 , c 2 ,…, c n ; свободные члены: b 1 , b 2 ,…, b m .
Двойственная задача линейного программирования имеет вид:
|
……………………….. |
В двойственной задаче требуется найти минимум целевой функции, ограничения – неравенства со знаком ≥, управляющие переменные y 1 , y 2 ,…, y m неотрицательны. Задача содержит m управляющих переменных и n ограничений. Коэффициенты целевой функции задачи b 1 , b 2 ,…, b m являются свободными членами исходной задачи линейного программирования, а свободные члены двойственной задачи c 1 , c 2 ,…, c n – коэффициентами целевой функции исходной задачи линейного программирования. Матрица коэффициентов двойственной задачи транспонирована, т.е. строки заменены столбцами, а столбцы – строками.
Задачи (9) –(10) и (11) – (12) образуют пару задач, называемую в линейном программировании двойственной парой.
Двойственная задача по отношению к исходной составляется по следующим правилам:
1. Целевая функция исходной задачи задается на максимум, а целевая функция двойственной – на минимум.
2. Матрица А (13)
|
|
составленная из коэффициентов при неизвестных в системе ограничений (10) исходной задачи (9) – (10) и аналогичная матрица в двойственной задаче (11) – (12) получаются друг из друга транспонированием.
3. Число переменных в двойственной задаче (11) – (12) равно числу ограничений в системе (10) исходной задачи, а число ограничений в системе (12) двойственной задачи – числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (11) двойственной задачи являются свободные члены в системе (10) исходной задачи, а правыми частями в ограничениях системы (12) двойственной задачи - коэффициенты при неизвестных в целевой функции (9) исходной задачи.
5. Если переменная x j исходной задачи (9) –(10) может принимать только лишь неотрицательные значения, то j - е ограничение в системе (12) двойственной задачи является неравенством вида ≥. Если же переменная x j может принимать как положительные, так и отрицательные значения, то j - е ограничение в системе (12) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (10) исходной задачи и переменными двойственной задачи. Если i - е ограничение в системе (10) исходной задачи является неравенством, то i - я переменная двойственной задачи y i ≥ 0. Если же i - е ограничение есть уравнение, то переменная y i может принимать как положительные, так и отрицательные значения.
Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирования – симплекс-метода. Геометрический смысл этого метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение (по отношению к цели задачи) до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум). Идеи метода были опубликованы российским ученым Л.В. Канторовичем в 1939 г.
Для применения симплекс-метода в ограничения задачи вводятся дополнительные переменные y 1 , y 2 ,…, y i и условие исходной задачи принимает вид:
|
……….………………….. |
Эту постановку можно представить в виде таблицы – первой таблицы симплекс-метода (табл. 1.1).
Таблица 1.1.
Первая симплекс-таблица
|
Свободные члены |
Свободные переменные |
||||
|
x 1 |
x 2 |
x n |
|||
|
y 1 |
b 1 |
a 11 |
a 12 |
a 1n |
|
|
y 2 |
b 2 |
a 21 |
a 22 |
a 2n |
|
|
y m |
b m |
a m1 |
a m2 |
a mn |
|
|
Индексная строка |
-c 1 |
-c 2 |
-c n |
||
Для составления симплекс-таблицы можно применить определенные правила.
1. Для первой таблицы:
а) в первый столбец записывают y m – базисные переменные, которые находятся в уравнениях слева;
б) свободные переменные a mn выносят в верхнюю строку таблицы;
в) в остальные столбцы записывают коэффициенты перед свободными переменными.
2. Для последующих таблиц:
а) выбирается наименьший отрицательный элемент в индексной строке при отыскании максимума, но наибольший положительный – при отыскании минимума, исключая вектор свободных членов;
б) этот элемент определяет ключевой вектор-столбец и он вводится в базис;
в) компоненты вектора свободных членов делятся на положительные элементы ключевого столбца;
г) из полученных отношений выбирается наименьшее;
д) вектор-строка, содержащая наименьшее положительное частное - ключевая и выводится из базиса;
е) на пересечении ключевых строк и столбца находится разрешающий элемент;
ж) преобразование матрицы:
Каждый элемент ключевой строки делится на разрешающий элемент. Полученные частные являются элементами ключевой строки следующей таблицы,
Ключевой столбец в новой таблице – нули, за исключением разрешающего элемента,
Остальные элементы новой таблицы рассчитываются по схеме:
Новый элемент = Старый элемент –
- Элемент ключевой строки*Элемент ключевого столбца
Разрешающий элемент
Если нулевая строка (столбец) содержит нуль, то соответствующий столбец (строка0 в новой таблице не изменится.
3. Пункты «а» - «ж» повторяются до тех пор, пока в индексной строке не останется ни одного отрицательного элемента при отыскании максимума (но ни одного положительного при отыскании минимума).
Пример 1.1. Требуется принять решение об оптимальном плане производства трикотажа на месяц на ОАО «Свияж» с применением симплекс-методы.
Определим план выпуска моделей мужского трикотажа с целью получения максимальной прибыли при заданных ресурсах с помощью построения математической модели. Исходные данные представлены в таблице 1.2.
Таблица 1.2.
Исходные данные
|
Ресурсы (i ) |
Вид продукции (j ) |
Запас ресурса (b i ) |
|||
|
Брюки спортивные модель 7060 |
Свитер мужской модель 55-1 |
Джемпер мужской модель 38-0 |
Костюм спортивный модель |
||
|
удельный расход ресурса (a ij ) |
|||||
|
Трудовые | |||||
|
Материальные | |||||
|
Оборудование | |||||
|
x 1 |
x 2 |
x 3 |
x 4 | ||
Исходные данные по удельному расходу материальных, трудовых ресурсов проставлены в табл. 1.2 в соответствии с действующей в организации нормативной и технологической документацией. По строке «Материальные ресурсы» зафиксирована норма расхода наиболее дефицитного (лимитируемого0 вида материалов – пряжа шерстяная. Этот материал имеет самую высокую норму расхода и стоимость.
По строке «Оборудование» проставлена сводная трудоемкость изготовления единицы изделия в нормо-часах как суммарная по всем детале-операциям. Остальные виды ресурсов также взяты в натуральных единицах: трудовые ресурсы – в часах; материальные – в дм 2 .
Строка «Прибыль» отражает прибыль от реализации единицы изделия, взята в из плановой калькуляции на единицу изделия.
Через x 1 , x 2 , x 3 , x 4 обозначили количество выпускаемой продукции каждого вида ассортимента.
Согласно правилу построения стандартной задачи линейного программирования составим математическую модель:
|
|
В ограничениях задачи введем дополнительные переменные y 1 , y 2 , y 3 и перепишем условие задачи в виде уравнения:
|
|
Последнюю постановку можно представить в виде таблицы 1.3 – первой таблицы симплекс-метода, которой воспользуемся для решения задачи линейного программирования.
Таблица 1.3.
Первая симплекс-таблица
|
Свободные члены |
Свободные переменные |
||||
|
x 1 |
x 2 |
x 3 |
x 4 |
||
|
y 1 | |||||
|
y 2 | |||||
|
y 3 | |||||
|
Индексная строка | |||||
В первый столбец записаны y i – базисные переменные, которые находятся в уравнении слева, а свободные переменные x j вынесены в верхнюю строку таблицы. В остальных столбцах записаны коэффициенты перед свободными переменными. Индексная строка – результат вычитания из нуля коэффициентов перед свободными переменными.
Для построения следующей таблицы выбирается наименьший отрицательный элемент в индексной строке (это 222). Этот элемент определяет ключевой вектор-столбец и он вводится в базис. Компоненты вектора свободных членов делятся на положительные элементы ключевого столбца и из полученных отношений выбирается наименьшее. Вектор-строка, содержащая наименьшее положительное частное, - ключевая и выводится из базиса (y 2 ). На пересечении ключевых строк и столбца находится разрешающий элемент (это 55,50).
Затем каждый элемент ключевой строки делится на разрешающий элемент. Полученные частные являются элементами ключевой строки следующей таблицы. В итоге получена вторая симплекс-таблица (табл. 1.4).
Таблица 1.4.
Вторая симплекс-таблица
|
Свободные члены |
Свободные переменные |
||||
|
x 1 |
x 2 |
x 3 |
x 4 |
||
|
y 1 | |||||
|
y 2 | |||||
|
y 3 | |||||
|
Индексная строка | |||||
Так как в индексной строке появился отрицательный элемент, следует повторить все аналогичные этапы и построить третью симплекс-таблицу.
В итоге получена табл. 1.5.
Таблица 1.5.
Итоговая симплекс-таблица
|
Свободные члены |
Свободные переменные |
||||
|
x 1 |
x 2 |
x 3 |
x 4 |
||
|
y 1 | |||||
|
y 2 | |||||
|
y 3 | |||||
|
Индексная строка | |||||
На
основании таблицы 1.5 можно сделать
выводы: в столбце свободных членов все
элементы положительны (это значит, что
полученное решение является допустимым);
в индексной строке все элементы также
положительны (это значит, что полученное
решение – оптимально, т.е. максимизирует
целевую функцию); оптимальным планом
будут величины:
 (значит,
они базисные);
(значит,
они базисные); (так
как они свободны); целевая функцияL
=
4 201 195.
(так
как они свободны); целевая функцияL
=
4 201 195.
Из таблицы 1.5 также следует, что базисная переменная y 3 =9716, а свободные переменные y 1 = y 2 = 0, т.е. в оптимальном плане резервы трудовых и материальных ресурсов равны нулю, так как они используются полностью. А резерв ресурсов оборудования y 2 = 9716, что свидетельствует о его излишках.
Таким образом, в результате применения метода линейного программирования принято решение о производстве джемперов мужских выбранной модели в количестве 3981 шт., свитеров мужских модели 55-1 в количестве 29 875 шт.
Линейное программирование сформировалось как отдельный раздел прикладной математики в 40 – 50-х гг. ХХ в. благодаря работам советского ученого, лауреата Нобелевской премии Л.В. Канторовича. В 1939 году им была опубликована работа «Математические методы организации и планирования производства», в которой он с использованием математики решил экономические задачи о наилучшей загрузке машин, раскрое материалов с наименьшими расходами, распределении грузов по нескольким видам транспорта и другие, предложив метод разрешающих множителей 8 .
Л.В. Канторович впервые сформулировал такие широко используемые экономико-математические понятия, как оптимальный план, оптимальное распределение ресурсов, объективно обусловленные оценки, указав многочисленные области экономики, где они могут быть применены.
Понятие линейного программирования было введено американским математиком Д. Данцигом, который в 1949 г. предложил алгоритм решения задачи линейного программирования, получивший название «симплексный метод».
Математическое программирование, в которое входит линейное программирование, в настоящее время является одним из направлений исследования операций. В зависимости от вида решаемых задач в нем выделяют такие области, как линейное, нелинейное, дискретное, динамическое программирование и др. Термин «программирование» введен в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу или план работы некоторого экономического объекта.
В классическом математическом анализе исследуются общая постановка задачи определения условного экстремума. Однако в связи с развитием промышленного производства, транспорта, агропромышленного комплекса, банковского сектора традиционных результатов математического анализа оказалось недостаточно. Потребности практики и развитие вычислительной техники привели к необходимости определения оптимальных решений при анализе сложных экономических систем.
Главным инструментом для решения таких задач является математическое моделирование. При этом сначала строится простая модель, затем проводится ее исследование, позволяющее понять, какие из интегрирующих свойств объекта не улавливаются формальной схемой, после чего за счет усложнения модели обеспечивается большая ее адекватность реальности. Во многих случаях первым приближением к действительности является модель, в которой все зависимости между переменными, характеризующими состояние объекта, являются линейными. Практика показывает, что достаточное количество экономических процессов достаточно полно описывается линейными моделями. Следовательно, линейное программирование как аппарат, позволяющий отыскивать условный экстремум на множестве, заданном линейными уравнениями и неравенствами, играет важную роль при анализе этих процессов.
Линейное программирование получило широкое развитие в связи с тем, что было установлено: ряд задач сферы планирования и управления может быть сформулирован в виде задач линейного программирования, для решения которых имеются эффективные методы. По оценкам специалистов примерно 80–85 % всех решаемых на практике задач оптимизации относится к задачам линейного программирования.
Созданный математический аппарат в сочетании с компьютерными программами, производящими трудоемкие расчеты, позволяет широко использовать модели линейного программирования в экономической науке и практике.
Определение 1 9 . Линейное программирование (ЛП) – это область математического программирования, являющегося разделом математики и изучающего методы поиска экстремальных (наибольших и наименьших) значений линейной функции конечного числа переменных, на неизвестные которой наложены линейные ограничения.
Эта линейная функция называется целевой, а ограничения, которые представляют количественные соотношения между переменными, выражающие условия и требования экономической задачи и математически записываются в виде уравнений или неравенств, называются системой ограничений.
К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения.
Общая задача линейного программирования (ЗЛП) состоит в нахождении экстремального значения (максимума или минимума) линейной функции, называемой целевой 10:
от n переменных x 1 , x 2 , …, х n при наложенных функциональных ограничениях:
 (3.2)
(3.2)
и прямых ограничениях (требовании неотрицательности переменных)
 , (3.3)
, (3.3)
где a ij , b i , c j – заданные постоянные величины.
В системе ограничений (3.2) знаки «меньше или равно», «равно», «больше или равно» могут встречаться одновременно.
ЗЛП в более краткой записи имеет вид:
 ,
,
при ограничениях:
 ;
;
 .
.
Вектор `Х = (x 1 , x 2 , …, х n ) компоненты которого удовлетворяют функциональным и прямым ограничениям задачи называют планом (или допустимым решением ) ЗЛП.
Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений (ОДР). Допустимое решение, которое доставляет максимум или минимум целевой функции f (`X ), называется оптимальным планом задачи и обозначается f (`X * ), где ` Х * =(x 1 * , x 2 * , …, х n * ).
Еще одна форма записи ЗЛП:

 ,
,
где f (`X * ) есть максимальное (минимальное) значение f (С , х ), взятое по всем решениям, входящим в множество возможных решений Х .
Определение 2 11 . Математическое выражение целевой функции и ее ограничений называются математической моделью экономической задачи.
Для составления математической модели необходимо:
1) обозначить переменные;
2) составить целевую функцию исходя из цели задачи;
3) записать систему ограничений, учитывая имеющие в условии задачи показатели и их количественные закономерности.
Линейное программирование рассматривается как революционное достижение, давшее человеку способность формулировать общие цели и находить посредством симплекс-метода оптимальные решения для широкого класса практических задач принятия решений большой сложности.
Линейное программирование – математическая дисциплина, посвящённая теории и методам решения задач об экстремумах линейных функций на множествах n -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира.
Задача линейного программирования (ЛП), состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
Линейное программирование применяется при решении следующих экономических задач:
1. Задача управления и планирования производства.
2. Задач определения оптимального размещения оборудования на морских судах, в цехах.
3. Задача определения оптимального плана перевозок груза (транспортная задача).
4. Задача оптимального распределения кадров.
5. Задач о смесях, диете (планирование состава продукции) и т.д.
3. МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ, ЕЁ ПРЕДСТАВЛЕНИЕ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ MS EXCEL.
Традиционно наукой управления называют построение детально разработанных моделей, в результате анализа которых принимаются управленческие решения. Сегодня миллионы менеджеров для анализа деловых задач применяют электронные таблицы. Современные электронные таблицы имеют много мощных средств, которые можно использовать для более точного анализа моделей, в результате чего могут приниматься более взвешенные и близкие к оптимальным решения. С учетом все более широкого применения электронных таблиц в процессе управления будущим специалистам необходимо владеть профессиональными навыкам разработки моделей – как «спланировать» чистый рабочий лист так, чтобы получить полезную и практическую модель деловой ситуации, не углубляясь в алгоритмические и математические тонкости расчетов.
Основные этапы создания модели линейного программирования в Excel:
1. Написание и проверка символической модели линейного программирования. Модель записывается на бумаге в математическом виде.
2. Создание и отладка табличной модели линейного программирования. На основе символической модели ЛП создается ее представление в Excel.
3. Попытка оптимизации модели с помощью надстройки ПОИСК РЕШЕНИЯ.
4. ИСПОЛЬЗОВАНИЕ НАДСТРОЙКИ ПОИСК РЕШЕНИЯ .
С помощью электронных таблиц можно моделировать реальные ситуации и оценивать полученные результаты. Другими словами с помощью электронных таблиц можно делать анализ результатов деятельности и прогнозирования будущих перспектив предприятия. Эти задачи в среде MS Excel дает возможность решать надстройка Поиск решения.
Поиск решения – это надстройка, которая предназначена для оптимизации моделей при наличии ограничений. Она состоит из двух программных компонентов: программы написанной на языке Visual Basic, который транслирует представленную на рабочем письме информацию для внутреннего представления, которая используется другой программой. Вторая программа находится в памяти компьютера в виде отдельного программного модуля. Она выполняет оптимизацию и возвращает найденное решение первой программе, которая возобновляет данные на рабочем листе. С помощью ее можно найти оптимальное значение формулы, которая сохраняется в целевой ячейке. Эта процедура работает с группой ячеек, которые непосредственно связанные с формулой в целевой ячейке. Чтобы получить результат по формуле в целевой ячейке, процедура изменяет значение в ячейках, которые влияют на поиск. Для того, чтобы уменьшить множественное число значений, которые используются в модели задачи, применяют ограничение. Эти ограничения могут содержать ссылку на другие ячейки, которые влияют на поиск.
Общий алгоритм работы с надстройкой Поиск решения.
- В меню Сервис выбрать команду Поиск решения .
- В поле Установит целевую ячейку введите адрес ячейки, в которй находится формула, для оптимизации модели.
- Для того, чтобы максимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение Максимальному значению . Для того, чтобы минимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение Минимальному значению . Для того, чтобы целевая ячейка приобретала значение конкретного числа, установите переключатель в положение Значение и введите соответствующее число.
- В поле Изменяя ячейки введите адреса ячеек, которые изменяют свои значения, разделяя их запятыми. Изменяемые ячейки должны быть прямо или непрямо связанные с целевой ячейкой. Допускается установка до 200 изменяемых ячеек.
- В поле Ограничения введите все ограничения, которые налагаются на поиск решения.
- Нажмите кнопку Выполнить .
- Для сохранения найденного решения установите переключатель в диалоговом окне Результаты поиска решения в положение Сохранить найденное решение . Для возобновления входных данных установите переключатель в положение Восстановить исходные значения.
- Для того, чтобы прервать поиск решения, нажмите клавишу Еsс . MS Excel пересчитает лист с учетом найденных значений ячеек, которые влияют на результат.
Алгоритм роботи з надбудовою Поиск решения.
5. РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ПОМОЩИ ПРОГРАММЫ MS EXCEL.
Пример. Кондитерский цех для изготовления трех видов карамели А, В, С использует три основных вида сырья: сахар, патоку и фруктовое пюре. Нормы затрат сахара на изготовление 1кг карамели каждого вида соответственно уровни: 0,8кг; 0,5кг; 0,6кг; патоки – 04кг; 0,4кг; 0,3кг; фруктового пюре – 0кг; 0,1кг; 0,1кг. Конфеты можно производить в любых количествах (реализация обеспечена), но запас сырья ограниченный: запасы сахара – 80кг, патоки – 60кг, фруктового пюре – 12кг. Прибыль от реализации 1кг карамели вида А составляет 10грн., вида В – 11грн., вида С – 12грн.
Таблица 1

Определить план производства карамели, которая обеспечивает максимальную прибыль от деятельности кондитерского цеха.







 ,
,